


Next: Calculation of Clebsch-Gordon Coefficients
Up: Addition of Angular Momentum
Previous: Commutation Rules
Clebsch-Gordon Coefficients
As we have seen, the operator group 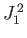 ,
, 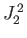 ,
, 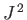 , and
, and 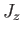 is incompatible with the group
is incompatible with the group 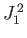 ,
, 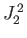 ,
, 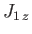 , and
, and 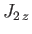 .
This means that if the system is in a simultaneous eigenstate of the former group
then, in general, it is not in a simultaneous eigenstate of the latter. In other words,
if the quantum numbers
.
This means that if the system is in a simultaneous eigenstate of the former group
then, in general, it is not in a simultaneous eigenstate of the latter. In other words,
if the quantum numbers 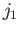 ,
,  ,
, 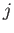 , and
, and  are known with
certainty then a measurement of the quantum numbers
are known with
certainty then a measurement of the quantum numbers  and
and 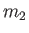 will
give a range of possible values. We can use the completeness relation
(6.20) to write
will
give a range of possible values. We can use the completeness relation
(6.20) to write
 |
(6.22) |
Thus, we can write the eigenkets of the first group of operators
as a weighted sum of the eigenkets of the second set. The weights,
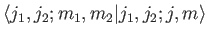 , are called the Clebsch-Gordon
coefficients. If the system is in a state where a measurement of
, are called the Clebsch-Gordon
coefficients. If the system is in a state where a measurement of
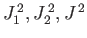 , and
, and 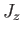 is bound to give the results
is bound to give the results
 ,
and
,
and
 , respectively, then a measurement of
, respectively, then a measurement of 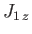 and
and 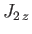 will give the results
will give the results
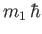 and
and
 , respectively, with
probability
, respectively, with
probability
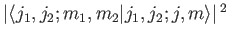 .
.
The Clebsch-Gordon coefficients possess a number of very important properties.
First, the coefficients are zero unless
 |
(6.23) |
To prove this, we note that
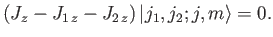 |
(6.24) |
Forming the inner product with
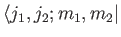 , we obtain
, we obtain
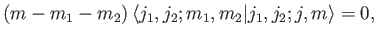 |
(6.25) |
which proves the assertion. Thus, the  -components of different angular momenta
add algebraically. So, an electron in an
-components of different angular momenta
add algebraically. So, an electron in an 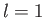 state, with orbital
angular momentum
state, with orbital
angular momentum 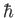 , and spin angular momentum
, and spin angular momentum 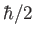 , projected along the
, projected along the
 -axis, constitutes a state whose total angular momentum projected
along the
-axis, constitutes a state whose total angular momentum projected
along the  -axis is
-axis is
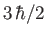 . What is uncertain is the magnitude of the
total angular momentum.
. What is uncertain is the magnitude of the
total angular momentum.
Second, the coefficients vanish unless
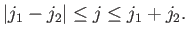 |
(6.26) |
We can assume, without loss of generality, that
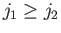 . We know,
from Equation (6.23), that for given
. We know,
from Equation (6.23), that for given
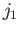 and
and  the largest possible value of
the largest possible value of  is
is  (because
(because
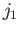 is the largest possible value of
is the largest possible value of  , etc.). This implies that
the largest possible value of
, etc.). This implies that
the largest possible value of 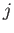 is
is  (because, by definition,
the largest value of
(because, by definition,
the largest value of  is equal to
is equal to 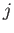 ).
Now, there are
).
Now, there are
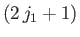 allowable values of
allowable values of  , and
, and
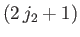 allowable
values of
allowable
values of 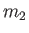 . Thus, there are
. Thus, there are
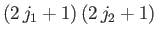 independent
eigenkets,
independent
eigenkets,
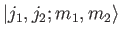 , needed to span the ket space
corresponding to fixed
, needed to span the ket space
corresponding to fixed 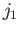 and
and  . Because the eigenkets
. Because the eigenkets
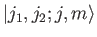 span the same space, they must also form
a set of
span the same space, they must also form
a set of
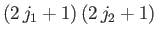 independent kets. In other words, there
can only be
independent kets. In other words, there
can only be
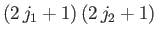 distinct allowable values of the quantum numbers
distinct allowable values of the quantum numbers
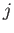 and
and  . For each allowed value of
. For each allowed value of 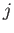 , there are
, there are 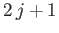 allowed values
of
allowed values
of  . We have already seen that the maximum allowed value of
. We have already seen that the maximum allowed value of 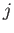 is
is
 . It is easily seen that if the minimum allowed value of
. It is easily seen that if the minimum allowed value of
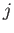 is
is 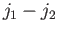 then the total number of allowed values of
then the total number of allowed values of 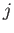 and
and  is
is
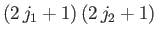 . In other words [59],
. In other words [59],
![$\displaystyle \sum_{j=j_1-j_2,j_1+j_2} (2\,j+1) = \left[(1+j)^2\right]_{j=j_1-j_2-1}^{j=j_1+j_2}=(2\,j_1+1)\,(2\,j_2+1).$](img1693.png) |
(6.27) |
This proves our assertion.
Third, the sum of the modulus squared of all of the Clebsch-Gordon coefficients
is unity: that is,
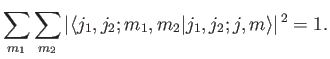 |
(6.28) |
This assertion is proved as follows:
where use has been made of the completeness relation (6.20).
Finally, the Clebsch-Gordon coefficients obey two recursion relations.
To obtain these relations, we start from
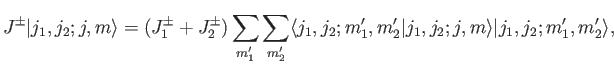 |
(6.29) |
where
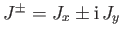 , et cetera,
Making use of the well-known properties of the ladder operators,
, et cetera,
Making use of the well-known properties of the ladder operators, 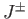 ,
, 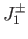 , and
, and 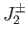 ,
which are specified by analogy with Equations (4.55)-(4.56), we obtain
,
which are specified by analogy with Equations (4.55)-(4.56), we obtain
Taking the inner product with
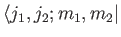 , and making
use of the orthonormality property of the basis eigenkets, we get
the desired recursion relations:
, and making
use of the orthonormality property of the basis eigenkets, we get
the desired recursion relations:
It is clear, from the absence of complex coupling coefficients in the previous relations,
that we can always choose the Clebsch-Gordon coefficients to be real numbers.
This is convenient, because it ensures that the inverse Clebsch-Gordon
coefficients,
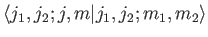 , are
identical to the Clebsch-Gordon coefficients. In other words,
, are
identical to the Clebsch-Gordon coefficients. In other words,
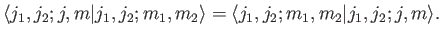 |
(6.30) |
The inverse Clebsch-Gordon coefficients are the weights in the expansion
of the
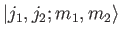 in terms of the
in terms of the
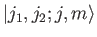 :
:
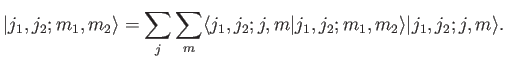 |
(6.31) |
It turns out that the recursion relations (6.32), together with the normalization
condition (6.28), are sufficient to completely determine the Clebsch-Gordon
coefficients to within an arbitrary sign (multiplied into
all of the coefficients). This sign is fixed by convention. [To be more exact, each Clebsch-Gordon sub-table
associated with a specific value of 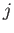 (see later)
is undetermined to an arbitrary sign. It is conventional to give the Clebsch-Gordon coefficient with the largest
value of
(see later)
is undetermined to an arbitrary sign. It is conventional to give the Clebsch-Gordon coefficient with the largest
value of  a positive sign.] The easiest
way of demonstrating this assertion is by considering a specific example.
a positive sign.] The easiest
way of demonstrating this assertion is by considering a specific example.



Next: Calculation of Clebsch-Gordon Coefficients
Up: Addition of Angular Momentum
Previous: Commutation Rules
Richard Fitzpatrick
2016-01-22


![$\displaystyle \sum_{j=j_1-j_2,j_1+j_2} (2\,j+1) = \left[(1+j)^2\right]_{j=j_1-j_2-1}^{j=j_1+j_2}=(2\,j_1+1)\,(2\,j_2+1).$](img1693.png)
![\begin{multline}
\langle j_1, j_2; j, m\vert j_1, j_2; j, m\rangle =\\ [0.5ex]
\...
...ert\langle j_1,j_2;m_1,m_2\vert j_1,j_2;j,m\rangle\vert^{\,2} =1,
\end{multline}](img1695.png)
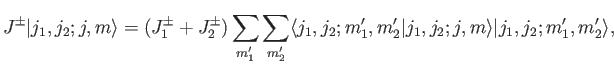
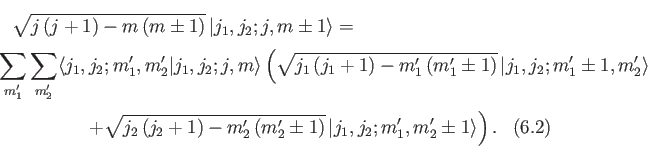
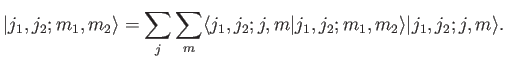
![]() (see later)
is undetermined to an arbitrary sign. It is conventional to give the Clebsch-Gordon coefficient with the largest
value of
(see later)
is undetermined to an arbitrary sign. It is conventional to give the Clebsch-Gordon coefficient with the largest
value of ![]() a positive sign.] The easiest
way of demonstrating this assertion is by considering a specific example.
a positive sign.] The easiest
way of demonstrating this assertion is by considering a specific example.