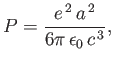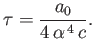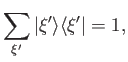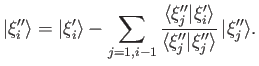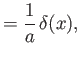Next: Position and Momentum
Up: Fundamental Concepts
Previous: Continuous Spectra
- According to the Larmor formula of classical physics, a non-relativistic electron whose instantaneous acceleration is of magnitude
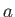 radiates
electromagnetic energy at the rate
radiates
electromagnetic energy at the rate
where 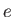 is the magnitude of the electron charge,
is the magnitude of the electron charge,
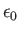 the permittivity of the vacuum,
and
the permittivity of the vacuum,
and 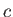 the velocity of light in vacuum [49]. Consider a classical electron in a
circular orbit of radius
the velocity of light in vacuum [49]. Consider a classical electron in a
circular orbit of radius 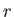 around a proton. Demonstrate that the radiated energy would cause the orbital radius to decrease in time according to
around a proton. Demonstrate that the radiated energy would cause the orbital radius to decrease in time according to
where
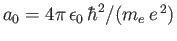 is the Bohr radius,
is the Bohr radius, 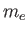 the
electron mass,
the
electron mass, 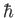 the reduced Planck constant, and
the reduced Planck constant, and
Here,
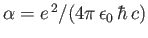 is the fine structure constant.
Deduce that the classical lifetime of a ground-state electron in a hydrogen atom is
is the fine structure constant.
Deduce that the classical lifetime of a ground-state electron in a hydrogen atom is
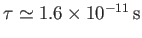 .
.
- Let the
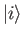 , for
, for 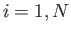 , be a set of orthonormal kets that span an
, be a set of orthonormal kets that span an 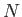 -dimensional ket space.
By orthonormal, we mean that the kets are mutually orthogonal, and have unit norms, so that
-dimensional ket space.
By orthonormal, we mean that the kets are mutually orthogonal, and have unit norms, so that
for 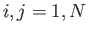 . Show that
. Show that
- Demonstrate that
in a finite-dimensional ket space.
- Demonstrate that in a finite-dimensional ket space:
Here, 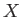 ,
, 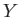 ,
, 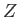 are general operators.
are general operators.
- If
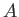 ,
, 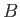 are Hermitian operators then demonstrate that
are Hermitian operators then demonstrate that 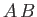 is only Hermitian provided
is only Hermitian provided 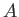 and
and 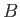 commute. In addition, show that
commute. In addition, show that  is Hermitian, where
is Hermitian, where  is a positive integer. [53]
is a positive integer. [53]
- Let
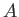 be a general operator. Show that
be a general operator. Show that 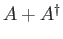 ,
,
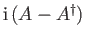 , and
, and 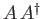 are Hermitian operators. [53]
are Hermitian operators. [53]
- Let
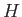 be an Hermitian operator. Demonstrate that the Hermitian conjugate of the operator
be an Hermitian operator. Demonstrate that the Hermitian conjugate of the operator
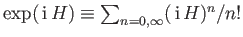 is
is
 . [53]
. [53]
- Suppose that
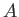 and
and 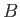 are two commuting operators. Demonstrate that
are two commuting operators. Demonstrate that
- Let the
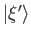 be the normalized eigenkets of an observable
be the normalized eigenkets of an observable  , whose corresponding eigenvalues,
, whose corresponding eigenvalues, 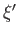 , are discrete.
Demonstrate that
, are discrete.
Demonstrate that
where the sum is over all eigenvalues.
- Let the
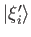 , where
, where 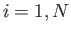 , and
, and 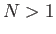 , be a set of degenerate unnormalized eigenkets of some
observable
, be a set of degenerate unnormalized eigenkets of some
observable  . Suppose that the
. Suppose that the
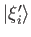 are not mutually orthogonal. Demonstrate that a set of
mutually orthogonal (but unnormalized) degenerate eigenkets,
are not mutually orthogonal. Demonstrate that a set of
mutually orthogonal (but unnormalized) degenerate eigenkets,
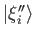 , for
, for 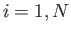 , can be constructed as follows:
, can be constructed as follows:
This process is known as Gram-Schmidt orthogonalization.
- Demonstrate that the expectation value of an Hermitian operator is a real number. Show that the
expectation value of an anti-hermitian operator is an imaginary number.
- Let
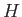 be an Hermitian operator. Demonstrate that
be an Hermitian operator. Demonstrate that
 .
.
- Consider an Hermitian operator,
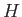 , that has the property that
, that has the property that 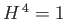 . What are the eigenvalues of
. What are the eigenvalues of 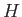 ? What are the eigenvalues if
? What are the eigenvalues if 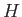 is not restricted to
being Hermitian? [53]
is not restricted to
being Hermitian? [53]
- An operator
 is said to be unitary if
is said to be unitary if
Show that if
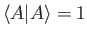 and
and
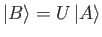 then
then
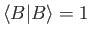 . [53]
. [53]
- Show that if
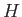 is Hermitian then
is Hermitian then
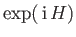 is unitary. [53]
is unitary. [53]
- Show that if the
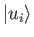 , for
, for 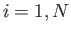 , form a complete orthonormal set, so that
, form a complete orthonormal set, so that
then the
 , for
, for 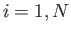 , where
, where  is unitary, are also orthonormal. [53]
is unitary, are also orthonormal. [53]
- The eigenstates of some operator
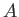 acting in an
acting in an 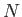 -dimensional ket space are written
-dimensional ket space are written
for 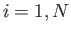 , where all of the
, where all of the  are real. Suppose that the
are real. Suppose that the 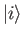 are orthonormal, and
span the ket space. Deduce that
are orthonormal, and
span the ket space. Deduce that 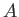 is Hermitian.
is Hermitian.
- Let
 be an observable whose eigenvalues,
be an observable whose eigenvalues, 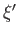 , lie in a continuous range. Let the
, lie in a continuous range. Let the
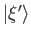 , where
, where
be the corresponding eigenkets. Demonstrate that
where the integral is over the whole range of eigenvalues.
- Show that
where 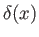 is a Dirac delta function, and
is a Dirac delta function, and 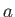 a constant.
a constant.



Next: Position and Momentum
Up: Fundamental Concepts
Previous: Continuous Spectra
Richard Fitzpatrick
2016-01-22