


Next: Compatible Observables
Up: Fundamental Concepts
Previous: Expectation Values
Suppose that two different (normalized) eigenstates
 and
and
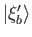 of the observable
of the observable  correspond to the same eigenvalue
correspond to the same eigenvalue 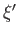 . These states are termed degenerate
eigenstates. Degenerate eigenstates are
necessarily orthogonal to any eigenstates corresponding to
different eigenvalues, but, in general, they are not orthogonal to each other
(i.e., the proof of orthogonality given in Section 1.8 does not work in this case).
This is unfortunate, because much of the previous formalism depends crucially
on the mutual orthogonality of the different eigenstates
of an observable. Note, however, that
any linear combination of
. These states are termed degenerate
eigenstates. Degenerate eigenstates are
necessarily orthogonal to any eigenstates corresponding to
different eigenvalues, but, in general, they are not orthogonal to each other
(i.e., the proof of orthogonality given in Section 1.8 does not work in this case).
This is unfortunate, because much of the previous formalism depends crucially
on the mutual orthogonality of the different eigenstates
of an observable. Note, however, that
any linear combination of
 and
and
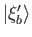 is also
an eigenstate corresponding to the eigenvalue
is also
an eigenstate corresponding to the eigenvalue 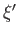 . It follows that we
can always construct two mutually orthogonal degenerate (normalized) eigenstates.
For instance,
. It follows that we
can always construct two mutually orthogonal degenerate (normalized) eigenstates.
For instance,
This result is easily generalized to the case of more than two degenerate eigenstates. (See Exercises 10.)
We conclude that it is always possible to construct a complete set of mutually
orthogonal eigenstates for any given observable.



Next: Compatible Observables
Up: Fundamental Concepts
Previous: Expectation Values
Richard Fitzpatrick
2016-01-22
![$\displaystyle =\frac{ \vert\xi_b'\rangle - \langle \xi_a'\vert\xi_b'\rangle \vert\xi_a'\rangle}{[1-\vert\langle \xi_a'\vert\xi_b'\rangle\vert^{\,2}]^{1/2}}.$](img164.png)
![$\displaystyle =\frac{ \vert\xi_b'\rangle - \langle \xi_a'\vert\xi_b'\rangle \vert\xi_a'\rangle}{[1-\vert\langle \xi_a'\vert\xi_b'\rangle\vert^{\,2}]^{1/2}}.$](img164.png)