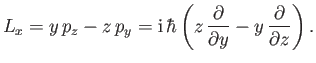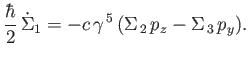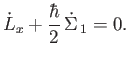Next: Motion in Central Field
Up: Relativistic Electron Theory
Previous: Free Electron Motion
Electron Spin
According to Equation (11.39), the relativistic Hamiltonian of an electron in an electromagnetic
field is
Hence,
![$\displaystyle \left(\frac{H}{c}+\frac{e}{c}\,\phi\right)^2 = \left[\mbox{\boldm...
...{\boldmath$\alpha$}\cdot({\bf p}+e\,{\bf A})\right]^{\,2} + m_e^{\,2}\,c^{\,2},$](img3988.png) |
(11.95) |
where use has been made of Equations (11.25) and (11.26).
Now, we can write
 |
(11.96) |
for 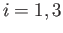 , where
, where
![$\displaystyle \gamma^{\,5} = \left(\begin{array}{cc} 0,& 1\\ [0.5ex]1, & 0\end{array}\right),$](img3990.png) |
(11.97) |
and
![$\displaystyle \Sigma_{\,i} = \left(\begin{array}{cc} \sigma_i,& 0\\ [0.5ex]0,& \sigma_i\end{array}\right).$](img3991.png) |
(11.98) |
Here, 0
and 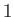 denote
denote 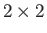 null and identity matrices, respectively, whereas the
null and identity matrices, respectively, whereas the 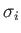 are conventional
are conventional
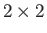 Pauli matrices. Note that
Pauli matrices. Note that
 , and
, and
![$\displaystyle [\gamma^{\,5}, \Sigma_{\,i}]=0.$](img3993.png) |
(11.99) |
It follows from Equation (11.95) that
![$\displaystyle \left(\frac{H}{c}+\frac{e}{c}\,\phi\right)^2 = \left[\mbox{\boldmath$\Sigma$}\cdot({\bf p}+e\,{\bf A})\right]^{\,2} + m_e^{\,2}\,c^{\,2}.$](img3994.png) |
(11.100) |
Now, a straightforward generalization of Equation (5.93) gives
where 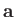 and
and 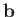 are any two three-dimensional vectors that commute with
are any two three-dimensional vectors that commute with
 .
It follows that
.
It follows that
![$\displaystyle \left[\mbox{\boldmath$\Sigma$}\cdot({\bf p}+e\,{\bf A})\right]^{\...
...,\mbox{\boldmath$\Sigma$}\cdot ({\bf p}+e\,{\bf A})\times ({\bf p}+e\,{\bf A}).$](img4000.png) |
(11.102) |
However,
where
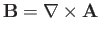 is the magnetic field-strength.
Hence, we obtain
is the magnetic field-strength.
Hence, we obtain
Consider the non-relativistic limit. In this case, we can write
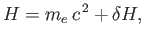 |
(11.105) |
where 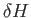 is small compared to
is small compared to
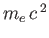 . Substituting into Equation (11.104), and neglecting
. Substituting into Equation (11.104), and neglecting
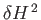 , and other
terms involving
, and other
terms involving 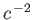 , we get
, we get
This Hamiltonian is the same as the classical Hamiltonian of a non-relativistic electron, except for the final term. (See Section 3.6.)
This term may be interpreted as arising from the electron having an intrinsic magnetic moment
(See Section 5.6.)
In order to demonstrate that the electron's intrinsic magnetic moment is associated with an intrinsic angular momentum,
consider the motion of an electron in a central electrostatic potential: that is,
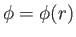 and
and
 .
In this case, the Hamiltonian (11.94) becomes
.
In this case, the Hamiltonian (11.94) becomes
Consider the  -component of the electron's orbital angular momentum,
-component of the electron's orbital angular momentum,
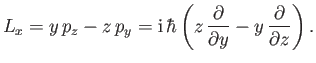 |
(11.109) |
The Heisenberg equation of motion for this quantity is
![$\displaystyle {\rm i}\,\hbar\,\dot{L}_x = [L_x,H].$](img4017.png) |
(11.110) |
However, it is easily demonstrated that
![$\displaystyle [L_x,r]$](img4018.png) |
 |
(11.111) |
![$\displaystyle [L_x,p_x]$](img4019.png) |
 |
(11.112) |
![$\displaystyle [L_x,p_y]$](img4020.png) |
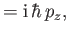 |
(11.113) |
![$\displaystyle [L_x,p_z]$](img4022.png) |
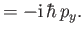 |
(11.114) |
Hence, we obtain
![$\displaystyle [L_x,H] = {\rm i}\,\hbar\,c\,\gamma^{\,5}\,(\Sigma_{\,2}\,p_z-\Sigma_{\,3}\,p_y),$](img4024.png) |
(11.115) |
which implies that
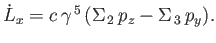 |
(11.116) |
It can be seen that 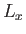 is not a constant of the motion. However, the
is not a constant of the motion. However, the  -component of the total angular
momentum of the system must be a constant of the motion (because a central electrostatic potential exerts zero torque on the system). Hence, we deduce that the electron possesses additional
angular momentum that is not connected with its motion through space. Now,
-component of the total angular
momentum of the system must be a constant of the motion (because a central electrostatic potential exerts zero torque on the system). Hence, we deduce that the electron possesses additional
angular momentum that is not connected with its motion through space. Now,
![$\displaystyle {\rm i}\,\hbar\,\dot{\Sigma}_{\,1}= [\Sigma_{\,1},H].$](img4026.png) |
(11.117) |
However,
![$\displaystyle [\Sigma_{\,1},\beta]$](img4027.png) |
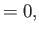 |
(11.118) |
![$\displaystyle [\Sigma_{\,1},\gamma^{\,5}]$](img4028.png) |
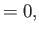 |
(11.119) |
![$\displaystyle [\Sigma_{\,1},\Sigma_{\,1}]$](img4029.png) |
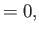 |
(11.120) |
![$\displaystyle [\Sigma_{\,1},\Sigma_{\,2}]$](img4030.png) |
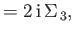 |
(11.121) |
![$\displaystyle [\Sigma_{\,1},\Sigma_{\,3}]$](img4032.png) |
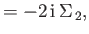 |
(11.122) |
so
![$\displaystyle [\Sigma_{\,1},H] = 2\,{\rm i}\,c\,\gamma^{\,5}\,(\Sigma_{\,3}\,p_y-\Sigma_{\,2}\,p_z),$](img4034.png) |
(11.123) |
which implies that
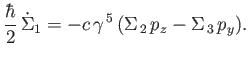 |
(11.124) |
Hence, we deduce that
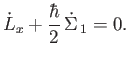 |
(11.125) |
Because there is nothing special about the  -direction, we conclude that the vector
-direction, we conclude that the vector
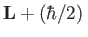
 is
a constant of the motion. We can interpret this result by saying that the electron has a spin angular momentum
is
a constant of the motion. We can interpret this result by saying that the electron has a spin angular momentum
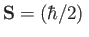
 , which must be added to its orbital angular momentum in order to obtain a constant of the motion.
According to Equation (11.107), the relationship between the electron's spin angular momentum and its intrinsic (i.e., non-orbital) magnetic moment is
, which must be added to its orbital angular momentum in order to obtain a constant of the motion.
According to Equation (11.107), the relationship between the electron's spin angular momentum and its intrinsic (i.e., non-orbital) magnetic moment is
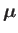  |
(11.126) |
where the gyromagnetic ratio,  , takes the value
, takes the value
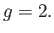 |
(11.127) |
As explained in Section 5.5, this is twice the value one would naively predict by analogy with classical physics.



Next: Motion in Central Field
Up: Relativistic Electron Theory
Previous: Free Electron Motion
Richard Fitzpatrick
2016-01-22
![$\displaystyle \gamma^{\,5} = \left(\begin{array}{cc} 0,& 1\\ [0.5ex]1, & 0\end{array}\right),$](img3990.png)
![$\displaystyle \left(\frac{H}{c}+\frac{e}{c}\,\phi\right)^2 = \left[\mbox{\boldmath$\Sigma$}\cdot({\bf p}+e\,{\bf A})\right]^{\,2} + m_e^{\,2}\,c^{\,2}.$](img3994.png)
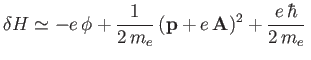
![]() and
and
![]() .
In this case, the Hamiltonian (11.94) becomes
.
In this case, the Hamiltonian (11.94) becomes