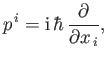Next: Dirac Equation
Up: Relativistic Electron Theory
Previous: Introduction
In the following, we shall employ
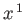 ,
, 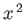 ,
, 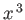 to represent the Cartesian coordinates
to represent the Cartesian coordinates  ,
,  ,
,  , respectively, and
, respectively, and  to represent
to represent  , where
, where 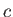 is the velocity of light in vacuum.
The time-dependent wavefunction then takes the form
is the velocity of light in vacuum.
The time-dependent wavefunction then takes the form
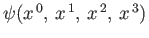 . Adopting
standard relativistic notation, we write the four
. Adopting
standard relativistic notation, we write the four  's as
's as 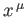 , for
, for
 [93]. A space-time
vector with four components that transform under Lorentz transformation in an analogous manner to the four space-time coordinates,
[93]. A space-time
vector with four components that transform under Lorentz transformation in an analogous manner to the four space-time coordinates,
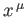 , is termed a 4-vector [93], and its components are written like
, is termed a 4-vector [93], and its components are written like 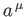 (i.e., with an upper
Greek suffix). We can lower the suffix according to the rules
(i.e., with an upper
Greek suffix). We can lower the suffix according to the rules
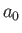 |
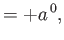 |
(11.1) |
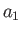 |
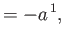 |
(11.2) |
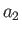 |
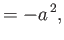 |
(11.3) |
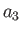 |
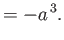 |
(11.4) |
Here, the 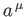 are called the contravariant components of the 4-vector
are called the contravariant components of the 4-vector 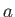 , whereas the
, whereas the
 are termed the covariant components. Two 4-vectors
are termed the covariant components. Two 4-vectors 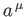 and
and 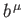 have the Lorentz-invariant scalar product
have the Lorentz-invariant scalar product
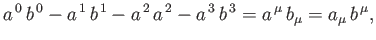 |
(11.5) |
a summation being implied over a repeated letter suffix [93]. The metric tenor,
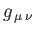 , is defined
, is defined
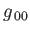 |
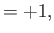 |
(11.6) |
 |
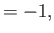 |
(11.7) |
 |
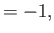 |
(11.8) |
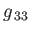 |
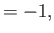 |
(11.9) |
with all other components zero [93].
Thus,
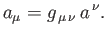 |
(11.10) |
Likewise,
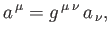 |
(11.11) |
where
 ,
,
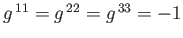 , with all other components zero.
Finally,
, with all other components zero.
Finally,
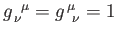 if
if 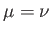 , and
, and
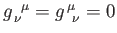 otherwise.
otherwise.
In the Schrödinger representation (see Section 2.4), the momentum of a particle, whose Cartesian components are written 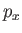 ,
, 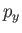 ,
, 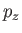 , or
, or 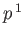 ,
, 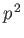 ,
, 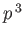 ,
is represented by the operators
,
is represented by the operators
 |
(11.12) |
for
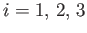 . Now, the four operators
. Now, the four operators
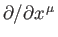 form the covariant components of a
4-vector whose contravariant components are written
form the covariant components of a
4-vector whose contravariant components are written
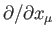 . (See Exercise 1.) So, to make
expression (11.12) consistent with relativistic theory, we must first write it with its
suffixes balanced,
. (See Exercise 1.) So, to make
expression (11.12) consistent with relativistic theory, we must first write it with its
suffixes balanced,
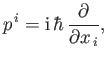 |
(11.13) |
and then extend it to the complete 4-vector equation,
 |
(11.14) |
where
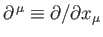 .
According to standard relativistic theory, the new operator
.
According to standard relativistic theory, the new operator
 , which forms a 4-vector when
combined with the momenta
, which forms a 4-vector when
combined with the momenta  , is interpreted as the energy of the particle divided by
, is interpreted as the energy of the particle divided by 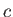 [93].
[93].



Next: Dirac Equation
Up: Relativistic Electron Theory
Previous: Introduction
Richard Fitzpatrick
2016-01-22
![]() ,
, ![]() ,
, ![]() , or
, or ![]() ,
, ![]() ,
, ![]() ,
is represented by the operators
,
is represented by the operators