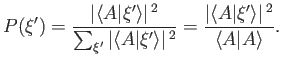Next: Expectation Values
Up: Fundamental Concepts
Previous: Observables
Measurements
We have seen that a measurement of some observable  of a microscopic
system causes the system to jump into one of the eigenstates of
of a microscopic
system causes the system to jump into one of the eigenstates of  . The
result of the measurement is the associated eigenvalue (or some function of
this quantity). It is impossible to determine into which eigenstate a
given system will jump, but it is possible to predict the probability of
such a transition. So, what is the probability that a system in some
initial state
. The
result of the measurement is the associated eigenvalue (or some function of
this quantity). It is impossible to determine into which eigenstate a
given system will jump, but it is possible to predict the probability of
such a transition. So, what is the probability that a system in some
initial state 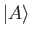 makes a transition to an eigenstate
makes a transition to an eigenstate
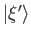 of an observable
of an observable  , as a result of a measurement made on the system?
Let us start with the simplest case. If the system is initially in an eigenstate
, as a result of a measurement made on the system?
Let us start with the simplest case. If the system is initially in an eigenstate
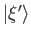 then the transition probability to a eigenstate
then the transition probability to a eigenstate
 corresponding to a different eigenvalue is zero, and the transition probability
to the same eigenstate
corresponding to a different eigenvalue is zero, and the transition probability
to the same eigenstate
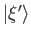 is unity. It is convenient to normalize
our eigenkets such that they all have unit norms. It follows from the
orthogonality property of the eigenkets that
is unity. It is convenient to normalize
our eigenkets such that they all have unit norms. It follows from the
orthogonality property of the eigenkets that
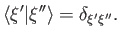 |
(1.53) |
For the moment, we are assuming that the eigenvalues of  are all different.
are all different.
Note that the probability of a transition from an initial eigenstate
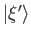 to a final eigenstate
to a final eigenstate
 is the same as
the value of the inner product
is the same as
the value of the inner product
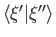 . Can we use this correspondence
to obtain a general rule for
calculating transition probabilities? Well, suppose that the system is initially
in a (normalized) state
. Can we use this correspondence
to obtain a general rule for
calculating transition probabilities? Well, suppose that the system is initially
in a (normalized) state 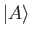 which is not an eigenstate of
which is not an eigenstate of  . Can we
identify the transition probability to a final eigenstate
. Can we
identify the transition probability to a final eigenstate
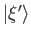 with
the inner product
with
the inner product
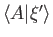 ? Unfortunately, this is not possible
because
? Unfortunately, this is not possible
because
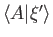 is, in general, a complex number, and complex
probabilities do not make any sense. Let us try again. Suppose that we
identify the transition probability with the modulus squared of the
inner product,
is, in general, a complex number, and complex
probabilities do not make any sense. Let us try again. Suppose that we
identify the transition probability with the modulus squared of the
inner product,
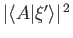 ? This
quantity is definitely a positive
number (so it could be a probability). This guess also gives the right answer for
the transition probabilities between eigenstates. In fact, it is the
correct guess.
? This
quantity is definitely a positive
number (so it could be a probability). This guess also gives the right answer for
the transition probabilities between eigenstates. In fact, it is the
correct guess.
Because the eigenstates of an observable  form a complete
set, we can express any given state
form a complete
set, we can express any given state 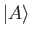 as a linear combination of them.
It is easily demonstrated that
as a linear combination of them.
It is easily demonstrated that
where the summation is over all the different eigenvalues of
 , and use has been
made of Equation (1.21), as well as
the fact that the eigenstates are mutually orthogonal. Note that all of the
previous results follow from the extremely useful result
, and use has been
made of Equation (1.21), as well as
the fact that the eigenstates are mutually orthogonal. Note that all of the
previous results follow from the extremely useful result
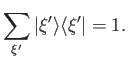 |
(1.57) |
(See Exercise 9.)
The relative
probability of a transition to an eigenstate
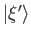 , which is
equivalent to
the relative probability of a measurement of
, which is
equivalent to
the relative probability of a measurement of  yielding the result
yielding the result 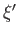 , is
, is
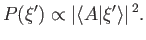 |
(1.58) |
The absolute probability
is clearly
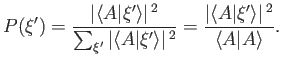 |
(1.59) |
If the ket 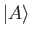 is normalized such that its norm is unity then this
probability simply reduces to
is normalized such that its norm is unity then this
probability simply reduces to
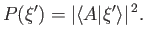 |
(1.60) |



Next: Expectation Values
Up: Fundamental Concepts
Previous: Observables
Richard Fitzpatrick
2016-01-22
![]() to a final eigenstate
to a final eigenstate
![]() is the same as
the value of the inner product
is the same as
the value of the inner product
![]() . Can we use this correspondence
to obtain a general rule for
calculating transition probabilities? Well, suppose that the system is initially
in a (normalized) state
. Can we use this correspondence
to obtain a general rule for
calculating transition probabilities? Well, suppose that the system is initially
in a (normalized) state ![]() which is not an eigenstate of
which is not an eigenstate of ![]() . Can we
identify the transition probability to a final eigenstate
. Can we
identify the transition probability to a final eigenstate
![]() with
the inner product
with
the inner product
![]() ? Unfortunately, this is not possible
because
? Unfortunately, this is not possible
because
![]() is, in general, a complex number, and complex
probabilities do not make any sense. Let us try again. Suppose that we
identify the transition probability with the modulus squared of the
inner product,
is, in general, a complex number, and complex
probabilities do not make any sense. Let us try again. Suppose that we
identify the transition probability with the modulus squared of the
inner product,
![]() ? This
quantity is definitely a positive
number (so it could be a probability). This guess also gives the right answer for
the transition probabilities between eigenstates. In fact, it is the
correct guess.
? This
quantity is definitely a positive
number (so it could be a probability). This guess also gives the right answer for
the transition probabilities between eigenstates. In fact, it is the
correct guess.
![]() form a complete
set, we can express any given state
form a complete
set, we can express any given state ![]() as a linear combination of them.
It is easily demonstrated that
as a linear combination of them.
It is easily demonstrated that