Next: Partial Waves
Up: Scattering Theory
Previous: Born Approximation
As we have seen, quantum scattering theory requires the solution of the integral
equation (10.29),
 |
(10.45) |
where
 is the incident wavefunction, and
is the incident wavefunction, and
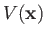 the scattering potential.
An obvious approach, in the weak-scattering limit, is to solve the preceding equation via a series of successive approximations. That is,
the scattering potential.
An obvious approach, in the weak-scattering limit, is to solve the preceding equation via a series of successive approximations. That is,
and so on.
Assuming that
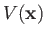 is only non-negligible relatively close to the origin, and taking the
limit
is only non-negligible relatively close to the origin, and taking the
limit
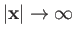 , we find that
, we find that
![$\displaystyle \psi({\bf x}) = \frac{1}{(2\pi)^{3/2}} \left[\exp(\,{\rm i}\,{\bf k}\cdot{\bf x}) + \frac{\exp(\,{\rm i}\,k\,r)}{r} f({\bf k}', {\bf k}) \right],$](img3448.png) |
(10.49) |
where
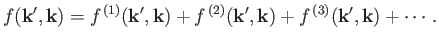 |
(10.50) |
The first two terms in the previous series, which is generally known as the Born expansion, are
Of course, we recognize Expression (10.51) as that produced by the Born approximation discussed in the preceding
section. In other words, the Born approximation essentially involves truncating the Born expansion after its first term.
Incidentally, it can be proved that the Born expansion converges for all 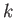 (for a spherically
symmetric scattering potential) provided; a)
(for a spherically
symmetric scattering potential) provided; a)
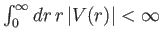 ; b)
; b)
 ; and; c)
; and; c) 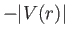 is too weak to form a bound state [19]. Furthermore, the criterion for convergence becomes
less stringent at high
is too weak to form a bound state [19]. Furthermore, the criterion for convergence becomes
less stringent at high 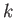 [69].
[69].



Next: Partial Waves
Up: Scattering Theory
Previous: Born Approximation
Richard Fitzpatrick
2016-01-22
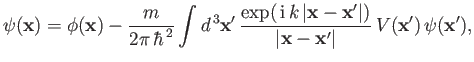
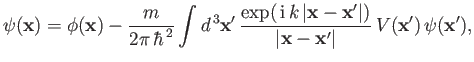
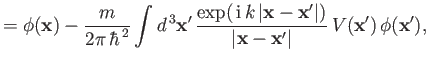
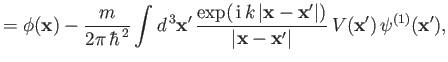
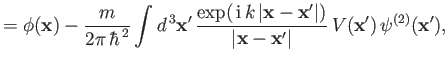
![$\displaystyle \psi({\bf x}) = \frac{1}{(2\pi)^{3/2}} \left[\exp(\,{\rm i}\,{\bf k}\cdot{\bf x}) + \frac{\exp(\,{\rm i}\,k\,r)}{r} f({\bf k}', {\bf k}) \right],$](img3448.png)