Next: Fourier Transformation Up: Linear Resonant Response Model Previous: Resonant Layer Equations Contents
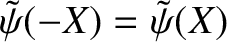 ,
,
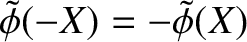 ,
,
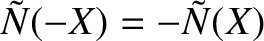 ,
,
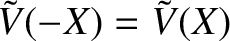 , and twisting parity solutions, characterized by the symmetry
, and twisting parity solutions, characterized by the symmetry
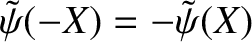 ,
,
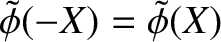 ,
,
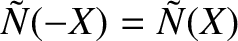 ,
,
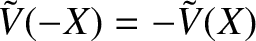 [16]. However, only the tearing parity
solutions can be asymptotically matched to tearing mode solutions in the outer region. If we assume that
the asymptotic behavior of the tearing parity layer solutions is such that
as
[16]. However, only the tearing parity
solutions can be asymptotically matched to tearing mode solutions in the outer region. If we assume that
the asymptotic behavior of the tearing parity layer solutions is such that
as
 , where
, where 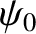 is an arbitrary constant, then asymptotic matching to the outer solution yields
[See Equations (3.72), (3.73), and (5.56).]
Furthermore, it follows from Equations (3.19) and (3.58)
that the asymptotic behavior of
is an arbitrary constant, then asymptotic matching to the outer solution yields
[See Equations (3.72), (3.73), and (5.56).]
Furthermore, it follows from Equations (3.19) and (3.58)
that the asymptotic behavior of
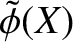 is
as
is
as
 , where
, where 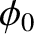 is an arbitrary constant,
is an arbitrary constant,