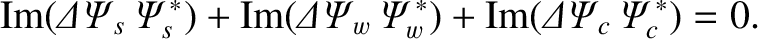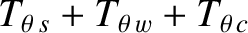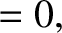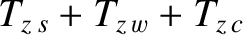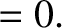Electromagnetic Torques
The flux-surface integrated poloidal and toroidal electromagnetic torque densities acting on the plasma
can be written
respectively,
where
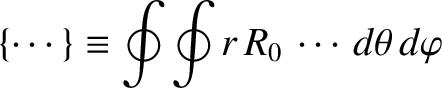 |
(3.131) |
is a flux-surface integration operator.
However, according to the equations of marginally-stable ideal-MHD, (2.375)–(2.380), both the plasma
equilibrium and the tearing perturbation satisfy the force balance criterion
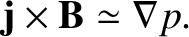 |
(3.132) |
Given that the scalar pressure is a single-valued function of 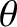 and
and 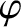 , it immediately follows
that
, it immediately follows
that
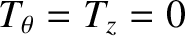 throughout the plasma [4]. The only exception to this rule occurs in the immediate vicinity of the
rational surface, where Equation (3.132) breaks down. It follows that we can write
where
are the net poloidal and toroidal torques, respectively, acting at the rational surface.
Note that the zeroth-order (in perturbed quantities) torques are zero because
throughout the plasma [4]. The only exception to this rule occurs in the immediate vicinity of the
rational surface, where Equation (3.132) breaks down. It follows that we can write
where
are the net poloidal and toroidal torques, respectively, acting at the rational surface.
Note that the zeroth-order (in perturbed quantities) torques are zero because 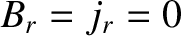 . Furthermore, the linear (in perturbed quantities) torques
average to zero over the flux-surface. Hence, the largest non-zero torques are quadratic in perturbed quantities.
. Furthermore, the linear (in perturbed quantities) torques
average to zero over the flux-surface. Hence, the largest non-zero torques are quadratic in perturbed quantities.
Now, it follows from Equations (3.32)–(3.38) that
The previous four equations yield [4]
where use has been made of Equations (3.72) and (3.73).
The net poloidal and toroidal electromagnetic torques acting on the resistive wall can be written
Making use of Equations (3.32), (3.82), and (3.105)–(3.107), we obtain [4]
The net poloidal and toroidal electromagnetic torques acting on the magnetic field-coil can be written
Making use of Equations (3.32), (3.109)–(3.111), (3.120), and (3.122), we obtain [4]
It follows from Equations (3.123)–(3.125) that
Thus,
However, according to Equations (3.90), (3.127), and (3.128),
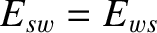 and
and
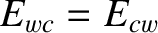 .
We deduce that
.
We deduce that
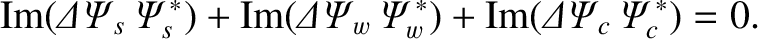 |
(3.153) |
Hence, Equations (3.139), (3.140), (3.143), (3.144), (3.147), and (3.148) yield [4]
In other words, the plasma/resistive wall/field-coil system exerts zero net poloidal electromagnetic torque, and zero net toroidal electromagnetic
torque, on itself.
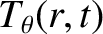
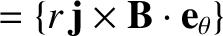
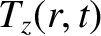
 and
and 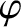 , it immediately follows
that
, it immediately follows
that
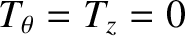 throughout the plasma [4]. The only exception to this rule occurs in the immediate vicinity of the
rational surface, where Equation (3.132) breaks down. It follows that we can write
where
are the net poloidal and toroidal torques, respectively, acting at the rational surface.
Note that the zeroth-order (in perturbed quantities) torques are zero because
throughout the plasma [4]. The only exception to this rule occurs in the immediate vicinity of the
rational surface, where Equation (3.132) breaks down. It follows that we can write
where
are the net poloidal and toroidal torques, respectively, acting at the rational surface.
Note that the zeroth-order (in perturbed quantities) torques are zero because 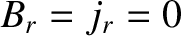 . Furthermore, the linear (in perturbed quantities) torques
average to zero over the flux-surface. Hence, the largest non-zero torques are quadratic in perturbed quantities.
. Furthermore, the linear (in perturbed quantities) torques
average to zero over the flux-surface. Hence, the largest non-zero torques are quadratic in perturbed quantities.
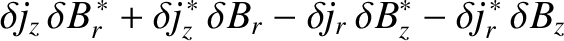
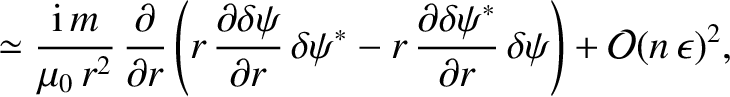
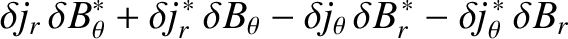
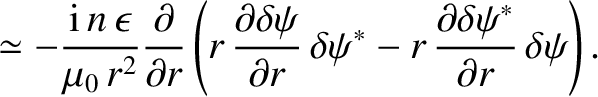
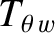
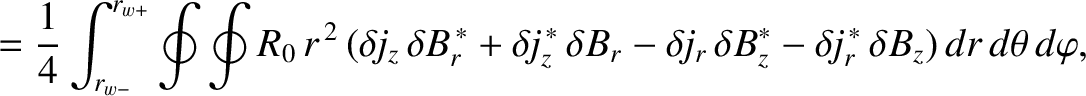
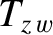
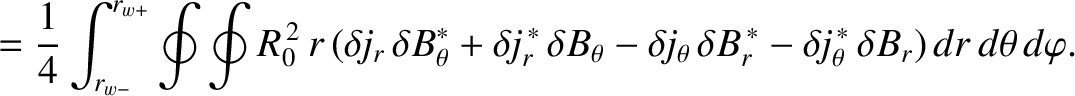
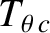
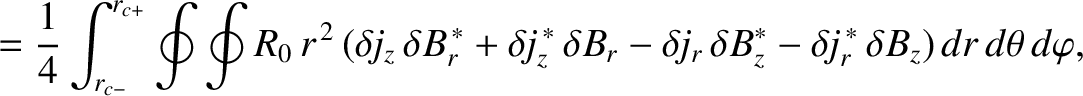
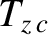
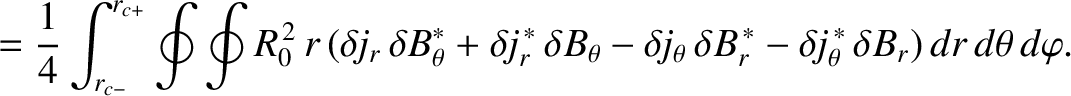
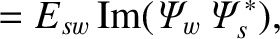
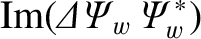
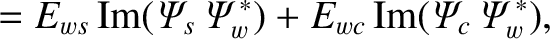
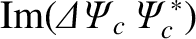
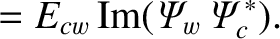
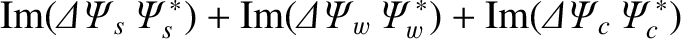
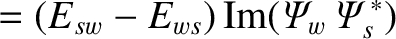
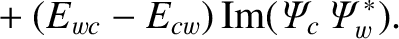
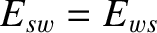 and
and
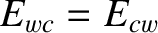 .
We deduce that
.
We deduce that