Next: Parallel Viscous Force Densities Up: Plasma Fluid Theory Previous: Useful Results Contents
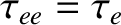 and
and
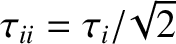 .
.
Our model expressions for the friction force densities,
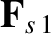 and
and
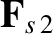 , are taken from the
moment-based analysis of Hirschman & Sigmar [24,34].
The ion friction force densities are written
, are taken from the
moment-based analysis of Hirschman & Sigmar [24,34].
The ion friction force densities are written
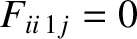 ,
,
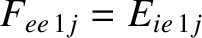 , and
, and
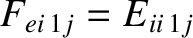 , for
, for 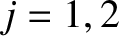 , ensuring that
which is a statement of collisional momentum conservation [18]. Note, further, that
, ensuring that
which is a statement of collisional momentum conservation [18]. Note, further, that
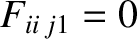 ,
,
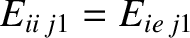 , and
, and
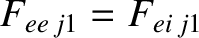 , for
, for 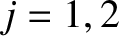 , which ensures that
, which ensures that
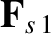 and
and
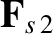 are
invariant under a Galilean transformation of the coordinate system.
are
invariant under a Galilean transformation of the coordinate system.