Next: Equilibrium Magnetic Field Up: Toroidal Tearing Modes Previous: Coordinate Systems Contents
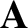 and
and 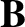 are arbitrary vector fields. Moreover, subscript/superscript
are arbitrary vector fields. Moreover, subscript/superscript 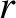 ,
, 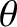 ,
, 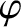 refer to covariant/contravariant
components of a vector in the
refer to covariant/contravariant
components of a vector in the 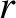 ,
, 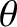 ,
, 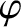 coordinate system.
coordinate system.