Low-Frequency Wave Propagation
Consider wave propagation through a magnetized plasma
at frequencies far below the ion cyclotron or plasma frequencies,
which are, in turn, well below the corresponding electron frequencies.
In the low-frequency limit (i.e.,
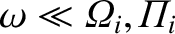 ),
we have [see Equations (5.28)–(5.30)]
Here, use has been made of
),
we have [see Equations (5.28)–(5.30)]
Here, use has been made of
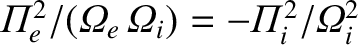 .
Thus, the eigenmode equation (5.42) reduces to
.
Thus, the eigenmode equation (5.42) reduces to
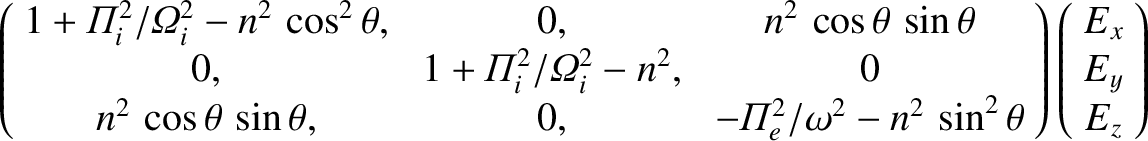 |
(5.77) |
The solubility condition for Equation (5.77) yields the dispersion relation
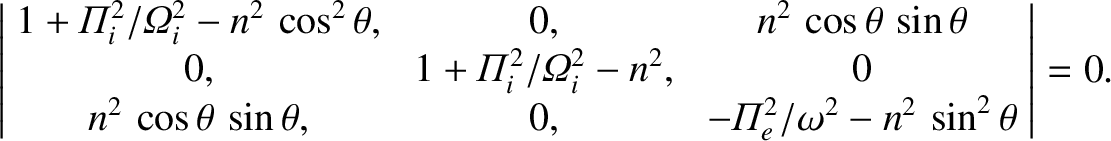 |
(5.78) |
Now, in the low-frequency ordering,
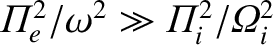 . Thus, we can see that the bottom
right-hand element of the previous determinant is far larger than any of the other
elements. Hence, to a good approximation, the roots of the dispersion relation
are obtained
by equating the term multiplying this large factor to zero (Cairns 1985). In this manner,
we obtain two roots:
. Thus, we can see that the bottom
right-hand element of the previous determinant is far larger than any of the other
elements. Hence, to a good approximation, the roots of the dispersion relation
are obtained
by equating the term multiplying this large factor to zero (Cairns 1985). In this manner,
we obtain two roots:
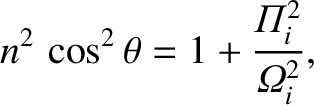 |
(5.79) |
and
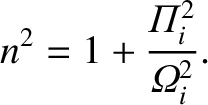 |
(5.80) |
It is fairly easy to show, from the definitions of the plasma and cyclotron
frequencies [see Equations (5.16)–(5.19)], that
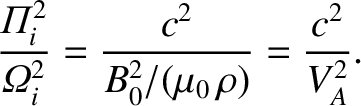 |
(5.81) |
Here,
 is the plasma mass density, and
is the plasma mass density, and
 |
(5.82) |
is known as the Alfvén velocity. Thus, the dispersion relations
(5.79) and (5.80) can be written
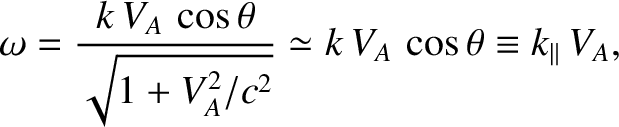 |
(5.83) |
and
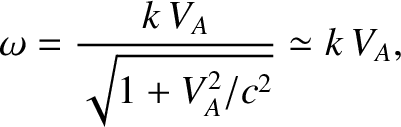 |
(5.84) |
respectively.
Here, we have made use of the fact that  in a conventional plasma.
in a conventional plasma.
The dispersion relation (5.83) corresponds to the slow or
shear-Alfvén wave, whereas the dispersion relation (5.84)
corresponds to the fast or compressional-Alfvén wave.
The fast/slow terminology simply refers to the relative magnitudes of the
phase-velocities of the two waves. The shear/compressional
terminology refers to the velocity fields associated with the waves. In
fact, it is clear from Equation (5.77) that 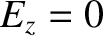 for both waves, whereas
for both waves, whereas
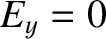 for the shear wave, and
for the shear wave, and 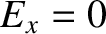 for the compressional wave.
Both waves are, in fact, MHD modes that satisfy the linearized MHD Ohm's law
[see Equation (4.196)]
for the compressional wave.
Both waves are, in fact, MHD modes that satisfy the linearized MHD Ohm's law
[see Equation (4.196)]
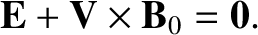 |
(5.85) |
Thus, for the shear wave
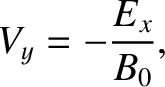 |
(5.86) |
and  , whereas for the compressional wave
, whereas for the compressional wave
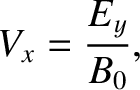 |
(5.87) |
and 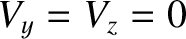 . Now,
. Now,
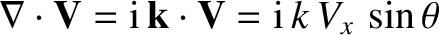 .
Thus, the shear-Alfvén wave is a torsional wave, with zero
divergence of the plasma flow, whereas the compressional wave involves a
non-zero flow divergence.
In fact, the former wave bends magnetic field-lines without
compressing them, whereas the latter compresses magnetic field-lines without
bending them (Hazeltine and Waelbroeck 2004).
It is important to realize that the
physical entity that resists compression in the compressional wave is the
magnetic field, not the plasma, because there is negligible plasma pressure in
the cold-plasma approximation.
.
Thus, the shear-Alfvén wave is a torsional wave, with zero
divergence of the plasma flow, whereas the compressional wave involves a
non-zero flow divergence.
In fact, the former wave bends magnetic field-lines without
compressing them, whereas the latter compresses magnetic field-lines without
bending them (Hazeltine and Waelbroeck 2004).
It is important to realize that the
physical entity that resists compression in the compressional wave is the
magnetic field, not the plasma, because there is negligible plasma pressure in
the cold-plasma approximation.
It should be noted that the thermal velocity is not necessarily negligible
compared to the Alfvén velocity in a conventional plasma. Thus,
we would expect the dispersion relations (5.83) and (5.84), for the shear- and compressional-Alfvén waves, respectively, to
undergo considerable modification in a “warm” plasma. (See Section 8.4.)
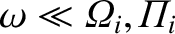 ),
we have [see Equations (5.28)–(5.30)]
),
we have [see Equations (5.28)–(5.30)]
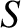
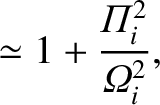
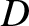
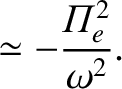
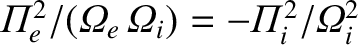 .
Thus, the eigenmode equation (5.42) reduces to
.
Thus, the eigenmode equation (5.42) reduces to
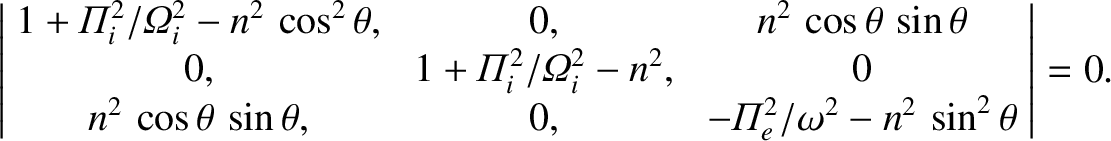
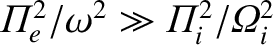 . Thus, we can see that the bottom
right-hand element of the previous determinant is far larger than any of the other
elements. Hence, to a good approximation, the roots of the dispersion relation
are obtained
by equating the term multiplying this large factor to zero (Cairns 1985). In this manner,
we obtain two roots:
and
. Thus, we can see that the bottom
right-hand element of the previous determinant is far larger than any of the other
elements. Hence, to a good approximation, the roots of the dispersion relation
are obtained
by equating the term multiplying this large factor to zero (Cairns 1985). In this manner,
we obtain two roots:
and
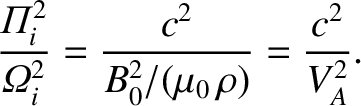
 is the plasma mass density, and
is the plasma mass density, and

 in a conventional plasma.
in a conventional plasma.
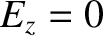 for both waves, whereas
for both waves, whereas
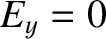 for the shear wave, and
for the shear wave, and 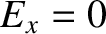 for the compressional wave.
Both waves are, in fact, MHD modes that satisfy the linearized MHD Ohm's law
[see Equation (4.196)]
for the compressional wave.
Both waves are, in fact, MHD modes that satisfy the linearized MHD Ohm's law
[see Equation (4.196)]
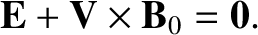
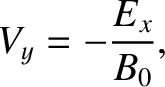
 , whereas for the compressional wave
, whereas for the compressional wave
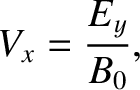
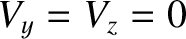 . Now,
. Now,
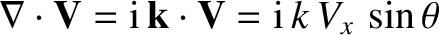 .
Thus, the shear-Alfvén wave is a torsional wave, with zero
divergence of the plasma flow, whereas the compressional wave involves a
non-zero flow divergence.
In fact, the former wave bends magnetic field-lines without
compressing them, whereas the latter compresses magnetic field-lines without
bending them (Hazeltine and Waelbroeck 2004).
It is important to realize that the
physical entity that resists compression in the compressional wave is the
magnetic field, not the plasma, because there is negligible plasma pressure in
the cold-plasma approximation.
.
Thus, the shear-Alfvén wave is a torsional wave, with zero
divergence of the plasma flow, whereas the compressional wave involves a
non-zero flow divergence.
In fact, the former wave bends magnetic field-lines without
compressing them, whereas the latter compresses magnetic field-lines without
bending them (Hazeltine and Waelbroeck 2004).
It is important to realize that the
physical entity that resists compression in the compressional wave is the
magnetic field, not the plasma, because there is negligible plasma pressure in
the cold-plasma approximation.