Next: WKB Solutions Up: Waves in Inhomogeneous Plasmas Previous: Waves in Inhomogeneous Plasmas Contents
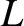 , of equilibrium quantities in the plasma is much longer than the
wavelength of the wave. In other words,
, of equilibrium quantities in the plasma is much longer than the
wavelength of the wave. In other words, 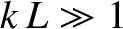 , where
, where 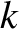 is the wavenumber. In this limit, we
expect our wave solutions to closely resemble those found in the previous chapter (recall that the latter solutions correspond to
is the wavenumber. In this limit, we
expect our wave solutions to closely resemble those found in the previous chapter (recall that the latter solutions correspond to
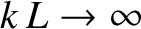 ). For the sake of simplicity, we shall (mostly) restrict our investigation to waves propagating
through unmagnetized plasmas. However, the techniques described in this chapter can be generalized, in a fairly straightforward
manner, to deal with other types of plasma wave (Budden 1985).
). For the sake of simplicity, we shall (mostly) restrict our investigation to waves propagating
through unmagnetized plasmas. However, the techniques described in this chapter can be generalized, in a fairly straightforward
manner, to deal with other types of plasma wave (Budden 1985).