Introduction

The cold-plasma equations describe waves (and other perturbations) that propagate through a plasma much faster than a typical thermal velocity. (See Section 4.12.) The collective motions described by the cold-plasma model are closely related to the individual particle motions discussed in Chapter 2. In fact, in the cold-plasma model, all particles (of a given species) at a given position effectively move with the same velocity. It follows that the fluid velocity is identical to the particle velocity, and is, therefore, governed by the same equations. However, the cold-plasma model goes beyond the single-particle description because it determines the electromagnetic fields self-consistently in terms of the charge and current densities generated by the particle motions. In this chapter, we shall use the cold-plasma equations to investigate the properties of small amplitude plasma waves.

What role, if any, does the geometry of the plasma equilibrium play in determining the properties of plasma waves? Clearly, geometry plays a key role for modes whose wavelengths are comparable to the dimensions of the plasma. However, it is plausible that waves whose wavelengths are much smaller than the plasma dimensions have properties that are, in a local sense, independent of the geometry. In other words, the local properties of small wavelength plasma oscillations are universal in nature. To investigate these properties, we can, to a first approximation, represent the plasma as a homogeneous equilibrium (corresponding to the limit 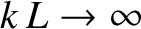$k\,L\rightarrow \infty$, where 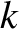$k$ is the magnitude of the wavevector, and 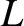$L$ is the characteristic equilibrium lengthscale).