Next: Exercises Up: Plasma Fluid Theory Previous: Langmuir Sheaths Contents
A Langmuir probe is a device used to determine the electron temperature and electron number density of a plasma. It works by inserting an electrode that is biased with respect to the vacuum vessel into the plasma. Provided that the bias voltage is not too positive, we would expect the probe current to vary as
where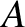 is the surface area of the probe, and
is the surface area of the probe, and 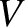 its bias with respect to the vacuum vessel. [See Equation (4.261).] This current-voltage relation is illustrated in Figure 4.5
For strongly negative
biases, the probe current saturates in the ion (negative) direction. The
characteristic current that flows in this situation is called the ion
saturation current, and is of magnitude
For less negative biases, the current-voltage relation of the probe
has the general form
its bias with respect to the vacuum vessel. [See Equation (4.261).] This current-voltage relation is illustrated in Figure 4.5
For strongly negative
biases, the probe current saturates in the ion (negative) direction. The
characteristic current that flows in this situation is called the ion
saturation current, and is of magnitude
For less negative biases, the current-voltage relation of the probe
has the general form
 |
(4.270) |
 is a constant. Thus, a plot of
is a constant. Thus, a plot of
 versus
versus 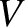 gives
a straight-line from whose slope the electron temperature can be deduced. Note, however, that if the bias voltage becomes too positive then
electrons cease to be effectively repelled from the probe surface, and the
current-voltage relation (4.268) breaks down.
Given the electron temperature, a measurement of the ion saturation current allows the electron
number density at the sheath edge,
gives
a straight-line from whose slope the electron temperature can be deduced. Note, however, that if the bias voltage becomes too positive then
electrons cease to be effectively repelled from the probe surface, and the
current-voltage relation (4.268) breaks down.
Given the electron temperature, a measurement of the ion saturation current allows the electron
number density at the sheath edge, 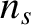 , to be calculated from Equation (4.269). Now, in order to accelerate ions to the Bohm velocity, the
potential drop across the pre-sheath needs to be
, to be calculated from Equation (4.269). Now, in order to accelerate ions to the Bohm velocity, the
potential drop across the pre-sheath needs to be
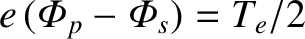 ,
where
,
where
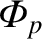 is the electric potential in the interior of the plasma. It follows
from Equation (4.249) that the relationship between the electron number
density at the sheath boundary,
is the electric potential in the interior of the plasma. It follows
from Equation (4.249) that the relationship between the electron number
density at the sheath boundary, 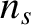 , and the number density in the interior of the plasma,
, and the number density in the interior of the plasma,  , is
, is
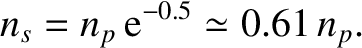 |
(4.271) |
 can also be determined from the probe.
can also be determined from the probe.