Next: Plasma Frequency Up: Plasma Parameters Previous: Brief History of Plasma Contents
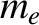 and charge
and charge 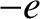 (here,
(here, 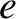 denotes the magnitude of the electron
charge), and ions, with mass
denotes the magnitude of the electron
charge), and ions, with mass 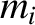 and charge
and charge 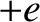 . Without necessarily
assuming that the system has attained thermal equilibrium, we shall employ
the symbol
. Without necessarily
assuming that the system has attained thermal equilibrium, we shall employ
the symbol
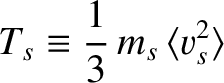 |
(1.1) |
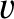 is a particle speed, and the angular brackets denote an
ensemble average (Reif 1965). The kinetic temperature of species
is a particle speed, and the angular brackets denote an
ensemble average (Reif 1965). The kinetic temperature of species  is a measure of
the mean kinetic energy of particles of
that species. (Here,
is a measure of
the mean kinetic energy of particles of
that species. (Here,  represents either
represents either 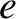 for electrons, or
for electrons, or 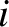 for ions.) In plasma physics, kinetic temperature
is invariably measured in electron-volts (1 joule is equivalent to
for ions.) In plasma physics, kinetic temperature
is invariably measured in electron-volts (1 joule is equivalent to
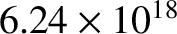 eV).
eV).
Quasi-neutrality demands that
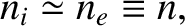 |
(1.2) |
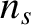 is the particle number density (that is, the number of particles
per cubic meter) of species
is the particle number density (that is, the number of particles
per cubic meter) of species  .
.
Assuming that both ions and electrons are characterized by the
same temperature, 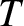 (which is, by no means, always the case in plasmas), we can
estimate typical particle speeds in terms of the so-called thermal speed,
(which is, by no means, always the case in plasmas), we can
estimate typical particle speeds in terms of the so-called thermal speed,
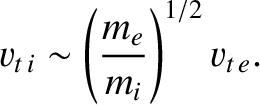 |
(1.4) |
Of course, 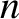 and
and 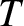 are generally functions of position in a plasma.
are generally functions of position in a plasma.