Next: Moments of Distribution Function Up: Plasma Fluid Theory Previous: Plasma Fluid Theory Contents
Fluid equations are conventionally obtained by taking velocity space moments of the kinetic equation (see Section 3.2),
Here, ,
,
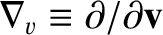 , and
, and
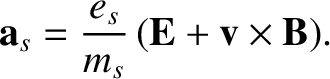 |
(4.2) |
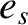 and
and 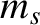 are the species-
are the species- electrical charge and mass, respectively, whereas
electrical charge and mass, respectively, whereas 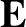 and
and 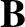 are the ensemble-averaged electromagnetic fields.
are the ensemble-averaged electromagnetic fields.
In general, it is extremely difficult to solve the kinetic equation directly, because of the complexity of the collision operator. However, there are some situations in which collisions can be completely neglected. In such cases, the kinetic equation simplifies to give the so-called Vlasov equation (Vlasov 1938),
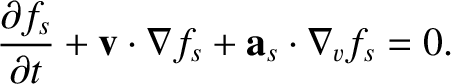 |
(4.3) |
First, fluid equations involve fewer dimensions than the Vlasov equation. That is, three spatial dimensions instead of six phase-space dimensions. This advantage is especially important in computer simulations.
Second, the fluid description is intuitively appealing. We immediately understand the significance of fluid quantities such as density and temperature, whereas the significance of distribution functions is far less obvious. Moreover, fluid variables are relatively easy to measure in experiments, whereas, in most cases, it is extraordinarily difficult to measure a distribution function accurately. There seems remarkably little point in centering our theoretical description of plasmas on something that we cannot generally measure.
Finally, the kinetic approach to plasma physics is spectacularly
inefficient. The species distribution functions 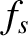 provide vastly more
information than is needed to obtain the constitutive relations [i.e., Equations (3.1) and (3.2)] that close Maxwell's equations. (See Section 3.2.)
After all, these relations only depend on the two lowest moments
of the species distribution functions.
provide vastly more
information than is needed to obtain the constitutive relations [i.e., Equations (3.1) and (3.2)] that close Maxwell's equations. (See Section 3.2.)
After all, these relations only depend on the two lowest moments
of the species distribution functions.