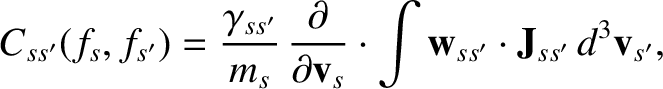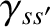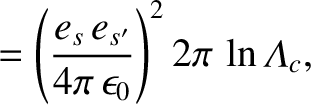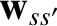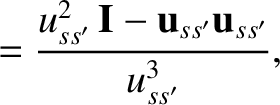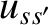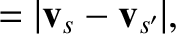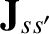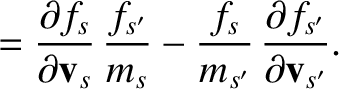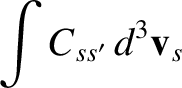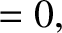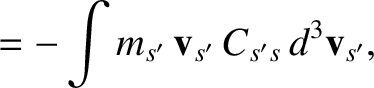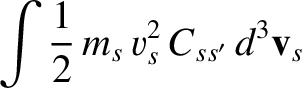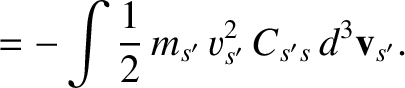- Consider the Maxwellian distribution
Demonstrate that
- The species-
 entropy per unit volume is conventionally defined as
entropy per unit volume is conventionally defined as
The Boltzmann H-theorem thus states that collisions drive the system toward a maximum entropy state
characterized by Maxwellian distribution functions with common mean velocities and common temperatures.
Demonstrate that for a Maxwellian distribution,
the entropy per unit volume takes the form
- The Landau collision operator is written
where
Demonstrate directly that this collision operator satisfies the same conservation laws as the Boltzmann collision operator. Namely,
![$\displaystyle f ({\bf v})= n\left(\frac{m}{2\pi\,T}\right)^{3/2}\,\exp\left[-\frac{m\,({\bf v}-{\bf V})^{2}}{2\,T}\right].
$](img982.png)
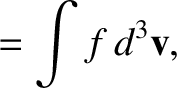
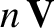
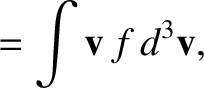
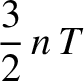
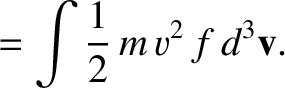
 entropy per unit volume is conventionally defined as
entropy per unit volume is conventionally defined as
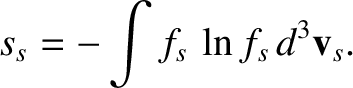

![$\displaystyle s_s= n_s\left[\ln\left(\frac{T_s^{3/2}}{n_s}\right) +\frac{3}{2}\ln\left(\frac{2\pi}{m_s}\right)+\frac{3}{2}\right].
$](img991.png)