Boltzmann H-Theorem
Consider a spatially uniform plasma in the absence of electromagnetic fields. The kinetic equation, (3.9), reduces to
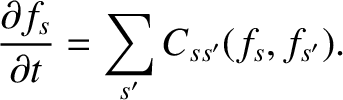 |
(3.123) |
Let us investigate the properties of this equation.
Consider the quantity
 |
(3.124) |
It follows from Equation (3.123) that
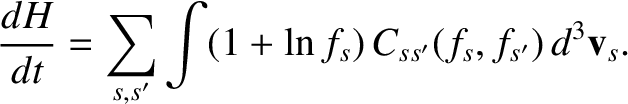 |
(3.125) |
Making use of the Boltzmann form of the collision operator, (3.23), the previous equation becomes
where
 is short-hand for
is short-hand for
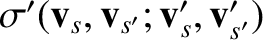 .
Suppose that we swap the dummy species labels
.
Suppose that we swap the dummy species labels  and
and  . This process leaves both
. This process leaves both
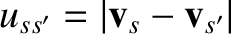 and the
value of the integral unchanged. According to Equation (3.27), it also
leaves the quantity
and the
value of the integral unchanged. According to Equation (3.27), it also
leaves the quantity
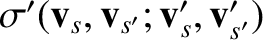 unchanged. Hence, we deduce that
unchanged. Hence, we deduce that
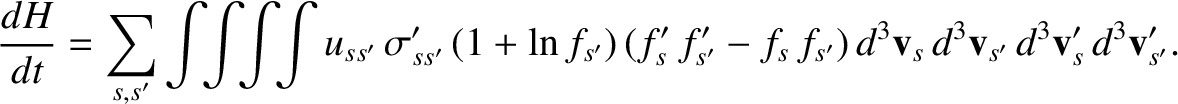 |
(3.127) |
Suppose that we swap primed and unprimed dummy variables of integration in Equation (3.126). This leaves the value of
the integral unchanged. Making use of Equation (3.18), as well as the fact that
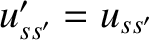 , we obtain
, we obtain
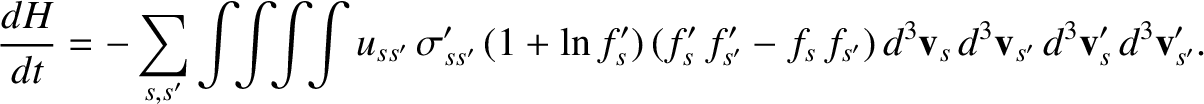 |
(3.128) |
Finally, swapping primed and unprimed variables in Equation (3.127) yields
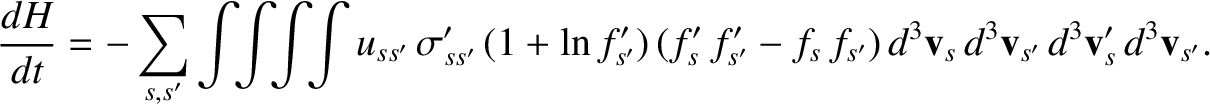 |
(3.129) |
The previous four equations can be combined to give
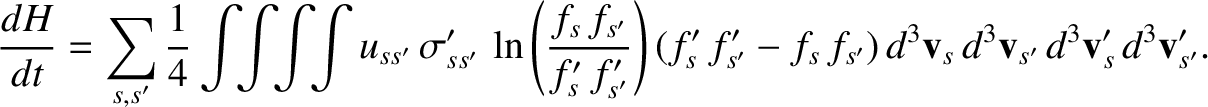 |
(3.130) |
Now,
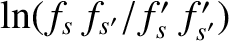 is positive when
is positive when
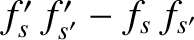 is negative, and vice versa. We, therefore, deduce that the integral
on the right-hand side of the previous expression can never take a positive value. In other words,
is negative, and vice versa. We, therefore, deduce that the integral
on the right-hand side of the previous expression can never take a positive value. In other words,
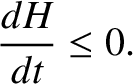 |
(3.131) |
This result is known as the Boltzmann H-theorem (Boltzmann 1995).
In fact, the quantity 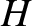 is bounded below (i.e., it cannot take the value minus infinity). Hence,
is bounded below (i.e., it cannot take the value minus infinity). Hence, 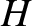 cannot
decrease indefinitely, but must tend to a limit in which
cannot
decrease indefinitely, but must tend to a limit in which 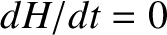 . According to
Equation (3.130), the distribution functions associated with this limiting state are characterized by
. According to
Equation (3.130), the distribution functions associated with this limiting state are characterized by
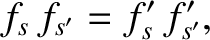 |
(3.132) |
or, equivalently,
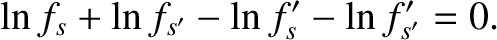 |
(3.133) |
Consider distribution functions that satisfy
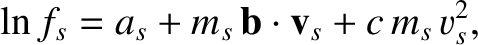 |
(3.134) |
where  is a species label,
is a species label, 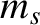 is the particle mass, and
is the particle mass, and  ,
, 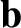 , and
, and 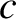 are constants.
It follows that
However, for an elastic collision, momentum conservation implies that (see Section 3.3)
are constants.
It follows that
However, for an elastic collision, momentum conservation implies that (see Section 3.3)
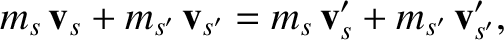 |
(3.136) |
whereas energy conservation yields (see Section 3.3)
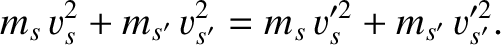 |
(3.137) |
In other words, distribution functions that satisfies Equation (3.134) automatically satisfy Equation (3.133). We, thus, conclude
that collisions act to drive the distribution functions for the colliding particles towards particular distribution functions
of the form (3.134). [Incidentally, elastic collisions generally only conserve particle number,
particle momentum, and particle energy. These conservation laws correspond to the three terms appearing on the right-hand side of Equation (3.134).
Hence, in the absence of other conservation laws, we can be sure that Equation (3.134) is the most general expression that satisfies Equation (3.133).]
Without loss of generality, we can set
where 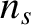 ,
, 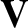 , and
, and 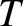 are constants. In this case, Equation (3.134) becomes
are constants. In this case, Equation (3.134) becomes
![$\displaystyle f_s= n_s\left(\frac{m_s}{2\pi\,T}\right)^{3/2}\,\exp\left[-\frac{m_s\,({\bf v}_s-{\bf V})^{2}}{2\,T}\right],$](img878.png) |
(3.141) |
which we recognize as a Maxwellian distribution function (Reif 1965). It is easily demonstrated that
These relations allow us to identify the constants 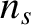 ,
, 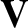 , and
, and 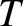 with the species-
with the species- number density, mean flow
velocity, and kinetic temperature, respectively. We conclude that collisions tend to relax the distribution functions of
the colliding particles toward Maxwellian distributions characterized by a common mean flow velocity and a common temperature.
number density, mean flow
velocity, and kinetic temperature, respectively. We conclude that collisions tend to relax the distribution functions of
the colliding particles toward Maxwellian distributions characterized by a common mean flow velocity and a common temperature.

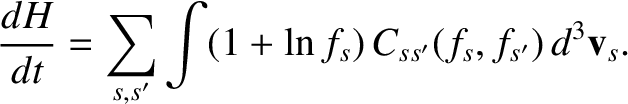
 is short-hand for
is short-hand for
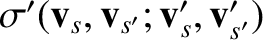 .
Suppose that we swap the dummy species labels
.
Suppose that we swap the dummy species labels  and
and 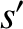 . This process leaves both
. This process leaves both
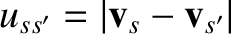 and the
value of the integral unchanged. According to Equation (3.27), it also
leaves the quantity
and the
value of the integral unchanged. According to Equation (3.27), it also
leaves the quantity
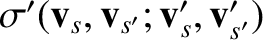 unchanged. Hence, we deduce that
Suppose that we swap primed and unprimed dummy variables of integration in Equation (3.126). This leaves the value of
the integral unchanged. Making use of Equation (3.18), as well as the fact that
unchanged. Hence, we deduce that
Suppose that we swap primed and unprimed dummy variables of integration in Equation (3.126). This leaves the value of
the integral unchanged. Making use of Equation (3.18), as well as the fact that
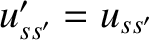 , we obtain
, we obtain
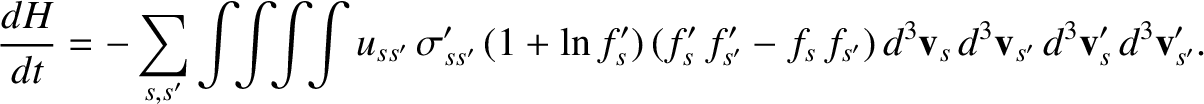
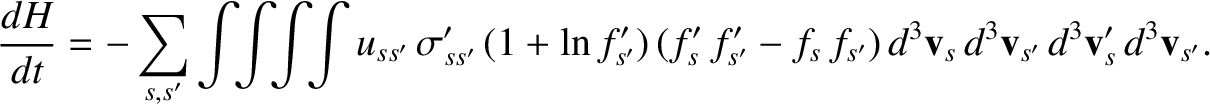
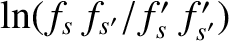 is positive when
is positive when
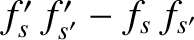 is negative, and vice versa. We, therefore, deduce that the integral
on the right-hand side of the previous expression can never take a positive value. In other words,
is negative, and vice versa. We, therefore, deduce that the integral
on the right-hand side of the previous expression can never take a positive value. In other words,
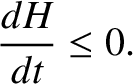
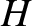 is bounded below (i.e., it cannot take the value minus infinity). Hence,
is bounded below (i.e., it cannot take the value minus infinity). Hence, 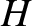 cannot
decrease indefinitely, but must tend to a limit in which
cannot
decrease indefinitely, but must tend to a limit in which 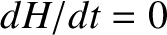 . According to
Equation (3.130), the distribution functions associated with this limiting state are characterized by
. According to
Equation (3.130), the distribution functions associated with this limiting state are characterized by
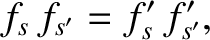
 is a species label,
is a species label,  is the particle mass, and
is the particle mass, and  ,
,  , and
, and 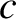 are constants.
It follows that
are constants.
It follows that

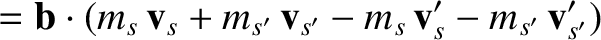

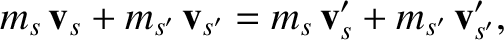
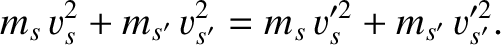
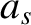
![$\displaystyle = \ln\left[n_s\,\left(\frac{m_s}{2\pi\,T}\right)^{3/2}\right] - \frac{m_s\,V^{2}}{2\,T},$](img873.png)
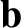



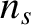 ,
, 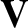 , and
, and 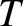 are constants. In this case, Equation (3.134) becomes
are constants. In this case, Equation (3.134) becomes
![$\displaystyle f_s= n_s\left(\frac{m_s}{2\pi\,T}\right)^{3/2}\,\exp\left[-\frac{m_s\,({\bf v}_s-{\bf V})^{2}}{2\,T}\right],$](img878.png)
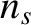
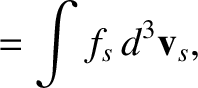
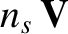
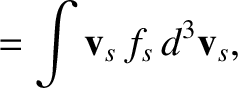
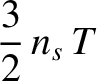

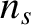 ,
, 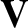 , and
, and 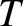 with the species-
with the species- number density, mean flow
velocity, and kinetic temperature, respectively. We conclude that collisions tend to relax the distribution functions of
the colliding particles toward Maxwellian distributions characterized by a common mean flow velocity and a common temperature.
number density, mean flow
velocity, and kinetic temperature, respectively. We conclude that collisions tend to relax the distribution functions of
the colliding particles toward Maxwellian distributions characterized by a common mean flow velocity and a common temperature.