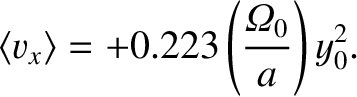Next: Collisions Up: Charged Particle Motion Previous: Third Adiabatic Invariant Contents
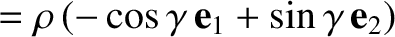 , and
, and
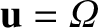
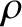
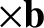 , where
, where
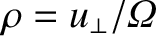 , and
, and
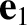 ,
, 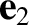 ,
,
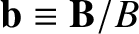 are a right-handed set of mutually perpendicular unit basis vectors, demonstrate that:
are a right-handed set of mutually perpendicular unit basis vectors, demonstrate that:
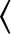
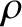

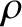

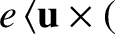
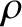
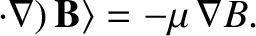
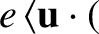
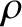
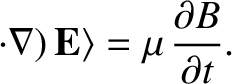
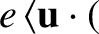
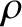

 , and
, and
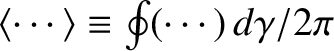 .
.
 ) plasma whose bounding surfaces are normal to the
) plasma whose bounding surfaces are normal to the  -axis consists of electrons of mass
-axis consists of electrons of mass 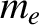 , charge
, charge  , and
mean number density
, and
mean number density 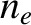 , as well as ions of mass
, as well as ions of mass  , charge
, charge 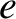 , and mean number density
, and mean number density 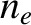 .
The slab is fully magnetized by a uniform
.
The slab is fully magnetized by a uniform  -directed magnetic field of magnitude
-directed magnetic field of magnitude  . The slab is then subject to an externally generated, uniform,
. The slab is then subject to an externally generated, uniform,  -directed
electric field that is gradually ramped up to a final magnitude
-directed
electric field that is gradually ramped up to a final magnitude 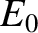 . Show
that, as a consequence of ion polarization drift, the final magnitude of the electric field inside the plasma is
. Show
that, as a consequence of ion polarization drift, the final magnitude of the electric field inside the plasma is
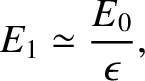
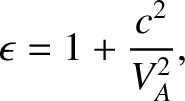
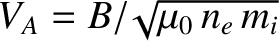 is the so-called Alfvén velocity.
is the so-called Alfvén velocity.
 -axis. The first wire lies at
-axis. The first wire lies at 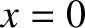 ,
, 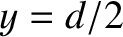 and carries a steady current
and carries a steady current  .
The second lies at
.
The second lies at 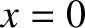 ,
, 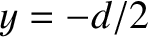 and carries a steady current
and carries a steady current 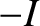 . Let
. Let
 and
and
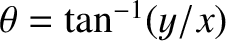 .
Demonstrate that the magnetic field generated by the dipole in the region
.
Demonstrate that the magnetic field generated by the dipole in the region 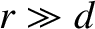 can be written
can be written
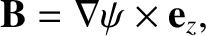
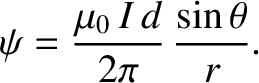
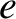 , mass
, mass 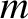 , and energy
, and energy  , trapped on a field-line of the linear magnetic
dipole discussed in the previous exercise. Let
, trapped on a field-line of the linear magnetic
dipole discussed in the previous exercise. Let
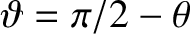 . Suppose that the field-line crosses the “equatorial” plane
. Suppose that the field-line crosses the “equatorial” plane
 at
at
 , and that the magnetic field-strength at this point is
, and that the magnetic field-strength at this point is
 .
Suppose that the particle's mirror points lie at
.
Suppose that the particle's mirror points lie at
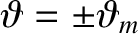 . Assume that the particle's gyroradius is much
smaller than
. Assume that the particle's gyroradius is much
smaller than
 , and that the electric field-strength is negligible.
, and that the electric field-strength is negligible.
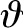 is
is
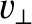 |
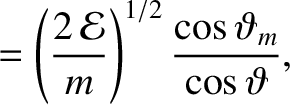 |
|
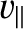 |
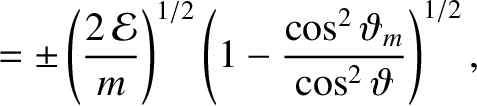 |
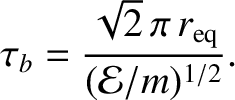
 -direction with the mean velocity
-direction with the mean velocity
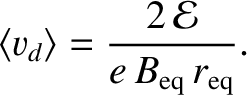
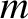 is trapped in a static magnetic mirror field given by
is trapped in a static magnetic mirror field given by

 , and pitch angle
, and pitch angle 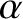 at
at 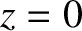 .
Assuming that the electric field is negligible, and that the particle's gyroradius is much less than
.
Assuming that the electric field is negligible, and that the particle's gyroradius is much less than 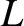 , use guiding center theory to show that
the bounce time is
, use guiding center theory to show that
the bounce time is

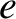 , mass
, mass 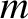 , and energy
, and energy  , is trapped in a one-dimensional magnetic well of the form
, is trapped in a one-dimensional magnetic well of the form
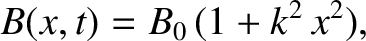
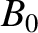 is constant, and
is constant, and 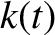 is a very slowly increasing function of time. Suppose that the particle's mirror
points lie at
is a very slowly increasing function of time. Suppose that the particle's mirror
points lie at
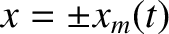 , and that its bounce time is
, and that its bounce time is 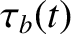 . Demonstrate that, as a consequence of the conservation of the first and second adiabatic
invariants,
. Demonstrate that, as a consequence of the conservation of the first and second adiabatic
invariants,
 |
![$\displaystyle = x_m(0)\left[\frac{k(0)}{k(t)}\right]^{1/2},$](img545.png) |
|
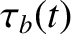 |
![$\displaystyle =\tau_b(0)\left[\frac{k(0)}{k(t)}\right],$](img547.png) |
|
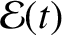 |
![$\displaystyle = {\cal E}_{0\,\perp} + \left[\frac{k(t)}{k(0)}\right]{\cal E}_{0\,\parallel}.$](img549.png) |
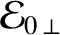 is the perpendicular energy [i.e.,
is the perpendicular energy [i.e.,
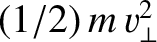 ], and
], and
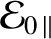 is the parallel energy [i.e.,
is the parallel energy [i.e.,
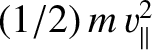 ], both evaluated at
], both evaluated at 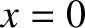 and
and 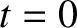 . Assume that the
particle's gyroradius is relatively small, and that the electric field-strength is negligible.
. Assume that the
particle's gyroradius is relatively small, and that the electric field-strength is negligible.
![\begin{displaymath}
B_z(y) = \left\{
\begin{array}{lll}
B_0&\mbox{\hspace{0.5cm}...
...a)&&\vert y\vert< a\\ [0.5ex]
-B_0 &&y < -a
\end{array}\right.
\end{displaymath}](img555.png)
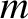 and charge
and charge 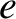 whose gyroradii,
whose gyroradii, 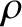 , are not necessarily much smaller than the shear-length,
, are not necessarily much smaller than the shear-length, 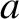 , of
the magnetic field. In this situation, guiding center theory is inapplicable.
The particles' orbits can only be analyzed by directly solving their
equations of perpendicular motion. It is easily demonstrated that some orbits
do not cross the neutral plane (
, of
the magnetic field. In this situation, guiding center theory is inapplicable.
The particles' orbits can only be analyzed by directly solving their
equations of perpendicular motion. It is easily demonstrated that some orbits
do not cross the neutral plane ( ) and resemble conventional
magnetized particle orbits, whereas others meander across the neutral
plane and are quite different from conventional orbits.
) and resemble conventional
magnetized particle orbits, whereas others meander across the neutral
plane and are quite different from conventional orbits.
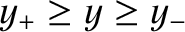 , where
, where
 .
Demonstrate that the mean drift velocity of the particle in the
.
Demonstrate that the mean drift velocity of the particle in the  -direction
can be written
-direction
can be written
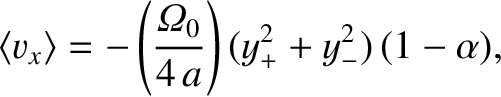
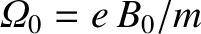 , and
, and
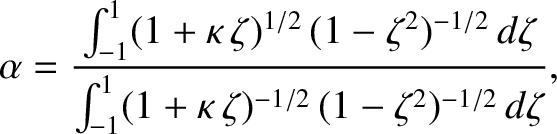
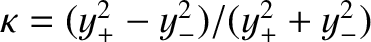 . Show that in
the limit
. Show that in
the limit
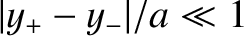 the previous result is consistent with that obtained
from conventional guiding center theory.
the previous result is consistent with that obtained
from conventional guiding center theory.
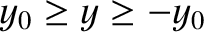 , where
, where 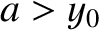 , and is
such that
, and is
such that 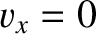 when
when  . Demonstrate that the mean drift velocity in
the
. Demonstrate that the mean drift velocity in
the  -direction is
-direction is