Van Allen Radiation Belts
Plasma confinement via magnetic mirroring occurs in nature. For instance, the Van Allen radiation belts,
which surround the Earth, consist of energetic particles trapped
in the Earth's dipole-like magnetic field. These belts were discovered by
James A. Van Allen and co-workers using data taken from Geiger counters
that flew on the early U.S. satellites, Explorer 1 (which was, in fact, the
first U.S. satellite), Explorer 4, and Pioneer 3. Van Allen was actually
trying to measure the flux of cosmic rays (high energy particles whose origin is
outside the solar system) in outer space, to see if it
was similar to that measured on Earth. However, the flux of energetic particles
detected by his instruments so greatly exceeded the expected value that it
prompted one of his co-workers, Ernie Ray, to exclaim, “My God, space is radioactive!” (Hess 1968).
It was quickly realized that this flux was due to energetic
particles trapped in the Earth's magnetic field, rather than to cosmic rays.
There are, in fact, two radiation belts surrounding the Earth (Baumjohan and Treumann 1996). The inner
belt, which extends from about 1–3 Earth radii in the equatorial plane,
is mostly populated by protons with energies exceeding 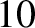 MeV. The origin of
these protons is thought to be the decay of neutrons that are emitted from
the Earth's atmosphere as it is bombarded by cosmic rays. The inner belt is fairly
quiescent. Particles eventually escape due to collisions with neutral atoms
in the upper atmosphere above the Earth's poles. However, such collisions
are sufficiently uncommon that the lifetime of particles in the inner belt range
from a few hours to 10 years. Obviously, with such long trapping
times, only a small input rate of energetic particles is required to produce a
region of intense radiation.
MeV. The origin of
these protons is thought to be the decay of neutrons that are emitted from
the Earth's atmosphere as it is bombarded by cosmic rays. The inner belt is fairly
quiescent. Particles eventually escape due to collisions with neutral atoms
in the upper atmosphere above the Earth's poles. However, such collisions
are sufficiently uncommon that the lifetime of particles in the inner belt range
from a few hours to 10 years. Obviously, with such long trapping
times, only a small input rate of energetic particles is required to produce a
region of intense radiation.
The outer belt, which extends from about 3–9 Earth radii in the equatorial
plane, consists mostly of electrons with energies below 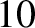 MeV. These electrons originate via injection from the outer magnetosphere. Unlike the
inner belt, the outer belt is very dynamic, changing on timescales of a few
hours in response to perturbations emanating from the outer magnetosphere.
MeV. These electrons originate via injection from the outer magnetosphere. Unlike the
inner belt, the outer belt is very dynamic, changing on timescales of a few
hours in response to perturbations emanating from the outer magnetosphere.
In regions not too far distant
(that is, less than 10 Earth radii) from the Earth, the geomagnetic field can be approximated
as a dipole field (see Figure 2.4),
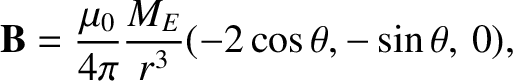 |
(2.91) |
where we have adopted conventional spherical coordinates
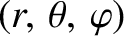 aligned
with the Earth's dipole moment, whose magnitude is
aligned
with the Earth's dipole moment, whose magnitude is
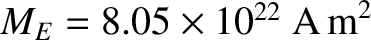 (Baumjohan and Treumann 1996). It is convenient to work in terms of the latitude,
(Baumjohan and Treumann 1996). It is convenient to work in terms of the latitude,
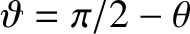 , rather than the polar angle,
, rather than the polar angle, 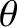 .
An individual magnetic field-line satisfies the equation
.
An individual magnetic field-line satisfies the equation
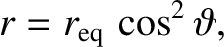 |
(2.92) |
where
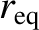 is the radial distance to the field-line in the equatorial
plane (
is the radial distance to the field-line in the equatorial
plane (
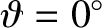 ). It is conventional to label field-lines
using the L-shell parameter,
). It is conventional to label field-lines
using the L-shell parameter,
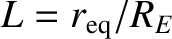 . Here,
. Here,
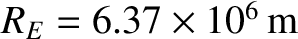 is the Earth's radius (Yoder 1995). Thus, the variation of the
magnetic field-strength along a field-line characterized by a given
is the Earth's radius (Yoder 1995). Thus, the variation of the
magnetic field-strength along a field-line characterized by a given 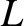 -value
is
-value
is
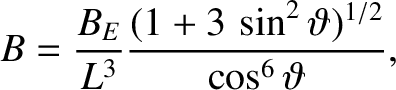 |
(2.93) |
where
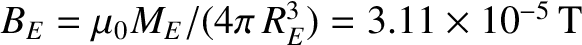 is the
equatorial magnetic field-strength on the Earth's surface (Baumjohan and Treumann 1996).
is the
equatorial magnetic field-strength on the Earth's surface (Baumjohan and Treumann 1996).
Consider, for the sake of simplicity, charged particles located
on the equatorial plane (
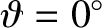 )
whose velocities are predominately directed perpendicular to the magnetic
field. The proton and electron gyrofrequencies are written2.1
)
whose velocities are predominately directed perpendicular to the magnetic
field. The proton and electron gyrofrequencies are written2.1
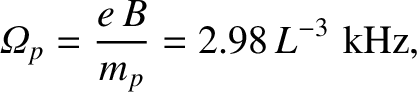 |
(2.94) |
and
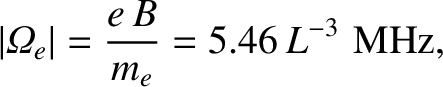 |
(2.95) |
respectively. The proton and electron gyroradii, expressed as fractions
of the Earth's radius, take the form
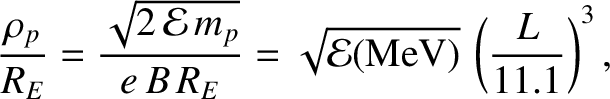 |
(2.96) |
and
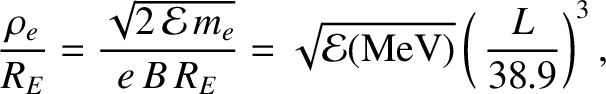 |
(2.97) |
respectively. Thus, MeV energy charged particles in the inner
magnetosphere (that is, 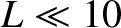 ) gyrate at frequencies that are much
greater than the typical rate of change of the magnetic field (which varies on
timescales that are, at most, a few minutes). Likewise, the gyroradii of
such particles are much smaller than the typical variation lengthscale
of the magnetospheric magnetic field.
Under these circumstances, we expect the magnetic moment
to be a conserved quantity. In other words, we expect the magnetic moment to be a good adiabatic invariant.
It immediately follows that any MeV energy protons and electrons in the inner magnetosphere
that have a
sufficiently large magnetic moment are trapped on the dipolar field-lines of the Earth's magnetic
field, bouncing back and forth between mirror points located just above
the Earth's poles.
) gyrate at frequencies that are much
greater than the typical rate of change of the magnetic field (which varies on
timescales that are, at most, a few minutes). Likewise, the gyroradii of
such particles are much smaller than the typical variation lengthscale
of the magnetospheric magnetic field.
Under these circumstances, we expect the magnetic moment
to be a conserved quantity. In other words, we expect the magnetic moment to be a good adiabatic invariant.
It immediately follows that any MeV energy protons and electrons in the inner magnetosphere
that have a
sufficiently large magnetic moment are trapped on the dipolar field-lines of the Earth's magnetic
field, bouncing back and forth between mirror points located just above
the Earth's poles.
It is helpful to define the pitch-angle,
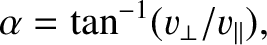 |
(2.98) |
of a charged particle in the magnetosphere. If the magnetic moment is
a conserved quantity then a particle of fixed energy drifting along a field-line
satisfies
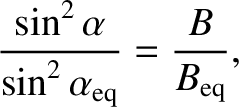 |
(2.99) |
where
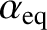 is the equatorial pitch-angle (that is, the
pitch-angle on the equatorial plane), and
is the equatorial pitch-angle (that is, the
pitch-angle on the equatorial plane), and
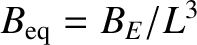 is the magnetic
field-strength on the equatorial plane. According to Equation (2.93), the
pitch-angle increases (i.e., the parallel component of the particle
velocity decreases)
as the particle drifts off the equatorial plane toward the Earth's
poles.
is the magnetic
field-strength on the equatorial plane. According to Equation (2.93), the
pitch-angle increases (i.e., the parallel component of the particle
velocity decreases)
as the particle drifts off the equatorial plane toward the Earth's
poles.
The mirror points correspond to
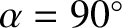 (i.e.,
(i.e.,
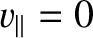 ).
It follows from Equations (2.93) and (2.99) that
).
It follows from Equations (2.93) and (2.99) that
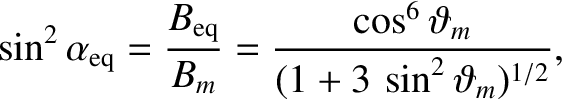 |
(2.100) |
where 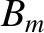 is the magnetic field-strength at the mirror points, and
is the magnetic field-strength at the mirror points, and
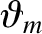 the latitude of the mirror points. It can be seen that the latitude of a particle's
mirror point depends only on its equatorial pitch-angle, and is independent
of the
the latitude of the mirror points. It can be seen that the latitude of a particle's
mirror point depends only on its equatorial pitch-angle, and is independent
of the 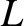 -value of the field-line on which it is trapped.
-value of the field-line on which it is trapped.
Charged particles with large equatorial pitch-angles have small parallel
velocities, and mirror points located at relatively low latitudes. Conversely,
charged particles with small equatorial pitch-angles have large parallel velocities,
and mirror points located at high latitudes. Of course, if the pitch-angle
becomes too small then the mirror points enter the Earth's atmosphere, and
the particles are lost via collisions with neutral particles.
Neglecting the thickness of the atmosphere with respect to
the radius of the Earth, we can say that all particles whose mirror points
lie inside the Earth are lost via collisions. It follows from
Equation (2.100) that the equatorial loss cone is of approximate width
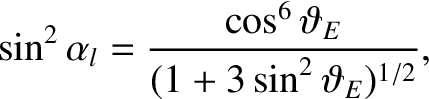 |
(2.101) |
where
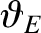 is the latitude of the point at which the magnetic field-line
under investigation intersects the Earth.
All particles with
is the latitude of the point at which the magnetic field-line
under investigation intersects the Earth.
All particles with
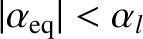 and
and
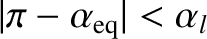 lie in the
loss cone.
According to Equation (2.92),
lie in the
loss cone.
According to Equation (2.92),
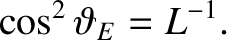 |
(2.102) |
It follows that
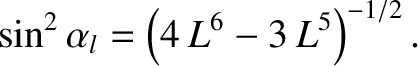 |
(2.103) |
Thus, the width of the loss cone is independent of the charge, the mass, or
the energy of the particles drifting along a given field-line,
and is a function only of the field-line radius
on the equatorial plane. The loss cone is surprisingly small. For instance,
at the radius of a geostationary satellite orbit (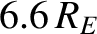 ), the loss cone is
less than
), the loss cone is
less than 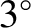 wide. The smallness of the
loss cone is a consequence of the very strong variation of the magnetic field-strength along field-lines in a dipole field. [See Equations (2.90) and (2.93).]
wide. The smallness of the
loss cone is a consequence of the very strong variation of the magnetic field-strength along field-lines in a dipole field. [See Equations (2.90) and (2.93).]
The bounce period, 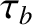 , is the time it takes a charged particle to move
from the equatorial plane to one mirror point, through the equatorial plane to the other mirror point, and then back
to the equatorial plane. It follows that
, is the time it takes a charged particle to move
from the equatorial plane to one mirror point, through the equatorial plane to the other mirror point, and then back
to the equatorial plane. It follows that
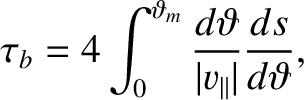 |
(2.104) |
where 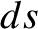 is an element of arc-length along the field-line under investigation,
and
is an element of arc-length along the field-line under investigation,
and
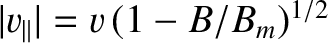 . The previous integral cannot
be performed analytically. However, it can be solved numerically, and is
conveniently approximated as (Baumjohan and Treumann 1996)
. The previous integral cannot
be performed analytically. However, it can be solved numerically, and is
conveniently approximated as (Baumjohan and Treumann 1996)
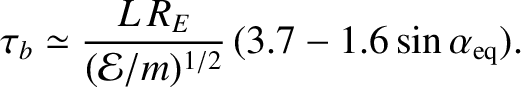 |
(2.105) |
Thus, for protons
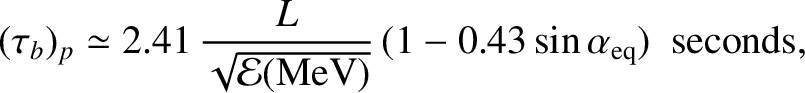 |
(2.106) |
while for electrons
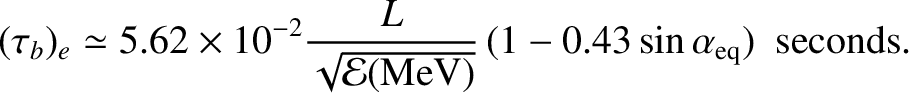 |
(2.107) |
It follows that MeV electrons typically have bounce periods that are less than
a second, whereas the bounce periods for MeV protons usually lie in the range 1 to
10 seconds. The bounce period only depends weakly on equatorial
pitch-angle, because particles with small pitch angles have relatively
large parallel velocities but a comparatively long way to travel to their
mirror points, and vice versa. Naturally, the bounce period
is longer for longer field-lines (that is, for larger 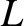 ).
).
 MeV. The origin of
these protons is thought to be the decay of neutrons that are emitted from
the Earth's atmosphere as it is bombarded by cosmic rays. The inner belt is fairly
quiescent. Particles eventually escape due to collisions with neutral atoms
in the upper atmosphere above the Earth's poles. However, such collisions
are sufficiently uncommon that the lifetime of particles in the inner belt range
from a few hours to 10 years. Obviously, with such long trapping
times, only a small input rate of energetic particles is required to produce a
region of intense radiation.
MeV. The origin of
these protons is thought to be the decay of neutrons that are emitted from
the Earth's atmosphere as it is bombarded by cosmic rays. The inner belt is fairly
quiescent. Particles eventually escape due to collisions with neutral atoms
in the upper atmosphere above the Earth's poles. However, such collisions
are sufficiently uncommon that the lifetime of particles in the inner belt range
from a few hours to 10 years. Obviously, with such long trapping
times, only a small input rate of energetic particles is required to produce a
region of intense radiation.
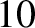 MeV. These electrons originate via injection from the outer magnetosphere. Unlike the
inner belt, the outer belt is very dynamic, changing on timescales of a few
hours in response to perturbations emanating from the outer magnetosphere.
MeV. These electrons originate via injection from the outer magnetosphere. Unlike the
inner belt, the outer belt is very dynamic, changing on timescales of a few
hours in response to perturbations emanating from the outer magnetosphere.
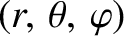 aligned
with the Earth's dipole moment, whose magnitude is
aligned
with the Earth's dipole moment, whose magnitude is
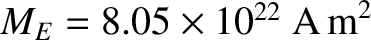 (Baumjohan and Treumann 1996). It is convenient to work in terms of the latitude,
(Baumjohan and Treumann 1996). It is convenient to work in terms of the latitude,
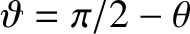 , rather than the polar angle,
, rather than the polar angle, 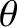 .
An individual magnetic field-line satisfies the equation
where
.
An individual magnetic field-line satisfies the equation
where
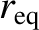 is the radial distance to the field-line in the equatorial
plane (
is the radial distance to the field-line in the equatorial
plane (
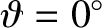 ). It is conventional to label field-lines
using the L-shell parameter,
). It is conventional to label field-lines
using the L-shell parameter,
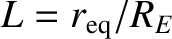 . Here,
. Here,
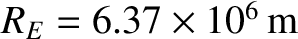 is the Earth's radius (Yoder 1995). Thus, the variation of the
magnetic field-strength along a field-line characterized by a given
is the Earth's radius (Yoder 1995). Thus, the variation of the
magnetic field-strength along a field-line characterized by a given  -value
is
where
-value
is
where
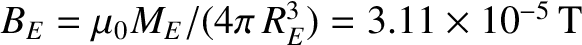 is the
equatorial magnetic field-strength on the Earth's surface (Baumjohan and Treumann 1996).
is the
equatorial magnetic field-strength on the Earth's surface (Baumjohan and Treumann 1996).
 )
whose velocities are predominately directed perpendicular to the magnetic
field. The proton and electron gyrofrequencies are written2.1
)
whose velocities are predominately directed perpendicular to the magnetic
field. The proton and electron gyrofrequencies are written2.1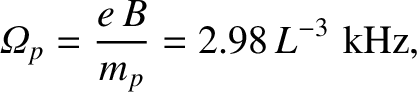
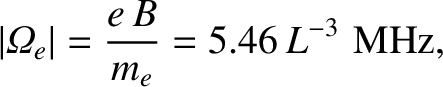
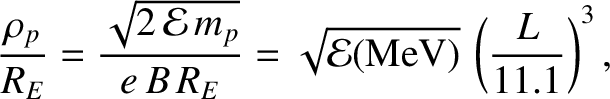
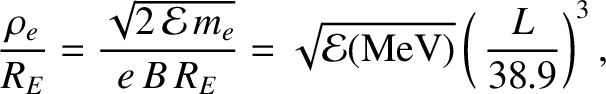
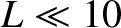 ) gyrate at frequencies that are much
greater than the typical rate of change of the magnetic field (which varies on
timescales that are, at most, a few minutes). Likewise, the gyroradii of
such particles are much smaller than the typical variation lengthscale
of the magnetospheric magnetic field.
Under these circumstances, we expect the magnetic moment
to be a conserved quantity. In other words, we expect the magnetic moment to be a good adiabatic invariant.
It immediately follows that any MeV energy protons and electrons in the inner magnetosphere
that have a
sufficiently large magnetic moment are trapped on the dipolar field-lines of the Earth's magnetic
field, bouncing back and forth between mirror points located just above
the Earth's poles.
) gyrate at frequencies that are much
greater than the typical rate of change of the magnetic field (which varies on
timescales that are, at most, a few minutes). Likewise, the gyroradii of
such particles are much smaller than the typical variation lengthscale
of the magnetospheric magnetic field.
Under these circumstances, we expect the magnetic moment
to be a conserved quantity. In other words, we expect the magnetic moment to be a good adiabatic invariant.
It immediately follows that any MeV energy protons and electrons in the inner magnetosphere
that have a
sufficiently large magnetic moment are trapped on the dipolar field-lines of the Earth's magnetic
field, bouncing back and forth between mirror points located just above
the Earth's poles.
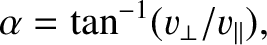
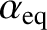 is the equatorial pitch-angle (that is, the
pitch-angle on the equatorial plane), and
is the equatorial pitch-angle (that is, the
pitch-angle on the equatorial plane), and
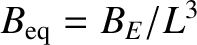 is the magnetic
field-strength on the equatorial plane. According to Equation (2.93), the
pitch-angle increases (i.e., the parallel component of the particle
velocity decreases)
as the particle drifts off the equatorial plane toward the Earth's
poles.
is the magnetic
field-strength on the equatorial plane. According to Equation (2.93), the
pitch-angle increases (i.e., the parallel component of the particle
velocity decreases)
as the particle drifts off the equatorial plane toward the Earth's
poles.
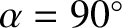 (i.e.,
(i.e.,
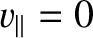 ).
It follows from Equations (2.93) and (2.99) that
).
It follows from Equations (2.93) and (2.99) that
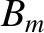 is the magnetic field-strength at the mirror points, and
is the magnetic field-strength at the mirror points, and
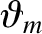 the latitude of the mirror points. It can be seen that the latitude of a particle's
mirror point depends only on its equatorial pitch-angle, and is independent
of the
the latitude of the mirror points. It can be seen that the latitude of a particle's
mirror point depends only on its equatorial pitch-angle, and is independent
of the 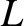 -value of the field-line on which it is trapped.
-value of the field-line on which it is trapped.
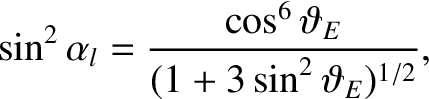
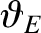 is the latitude of the point at which the magnetic field-line
under investigation intersects the Earth.
All particles with
is the latitude of the point at which the magnetic field-line
under investigation intersects the Earth.
All particles with
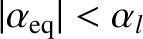 and
and
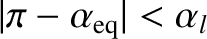 lie in the
loss cone.
According to Equation (2.92),
lie in the
loss cone.
According to Equation (2.92),
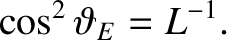
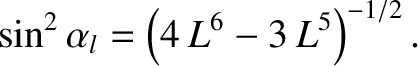
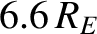 ), the loss cone is
less than
), the loss cone is
less than 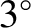 wide. The smallness of the
loss cone is a consequence of the very strong variation of the magnetic field-strength along field-lines in a dipole field. [See Equations (2.90) and (2.93).]
wide. The smallness of the
loss cone is a consequence of the very strong variation of the magnetic field-strength along field-lines in a dipole field. [See Equations (2.90) and (2.93).]
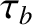 , is the time it takes a charged particle to move
from the equatorial plane to one mirror point, through the equatorial plane to the other mirror point, and then back
to the equatorial plane. It follows that
, is the time it takes a charged particle to move
from the equatorial plane to one mirror point, through the equatorial plane to the other mirror point, and then back
to the equatorial plane. It follows that
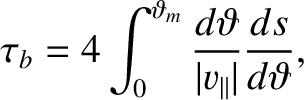
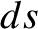 is an element of arc-length along the field-line under investigation,
and
is an element of arc-length along the field-line under investigation,
and
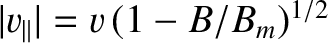 . The previous integral cannot
be performed analytically. However, it can be solved numerically, and is
conveniently approximated as (Baumjohan and Treumann 1996)
. The previous integral cannot
be performed analytically. However, it can be solved numerically, and is
conveniently approximated as (Baumjohan and Treumann 1996)
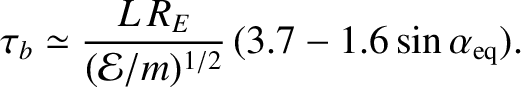
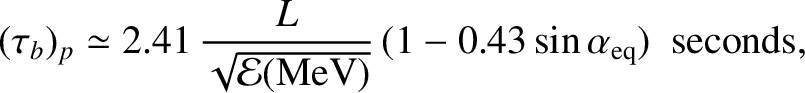
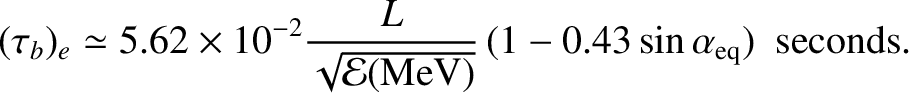
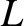 ).
).