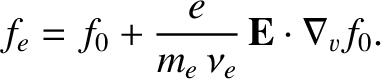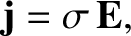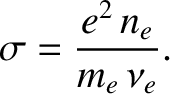Next: Waves in Cold Plasmas Up: Plasma Fluid Theory Previous: Langmuir Probes Contents
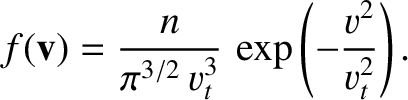
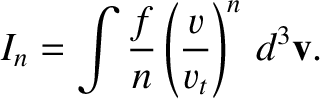
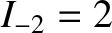 ,
, 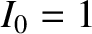 ,
,  , and
, and  .
.
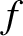 satisfies the simplified kinetic equation
satisfies the simplified kinetic equation
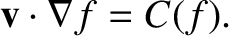
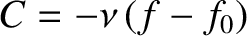
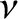 is the effective collision frequency, and
is the effective collision frequency, and
![$\displaystyle f_0 = \frac{n}{\pi^{3/2}\,v_t^{3}}\exp\left[-\frac{({\bf v}-{\bf V})^{2}}{v_t^{2}}\right].
$](img1636.png)
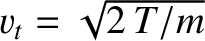 . Suppose that the mean-free-path
. Suppose that the mean-free-path  is
much less than the typical variation lengthscale of equilibrium quantities
(such as
is
much less than the typical variation lengthscale of equilibrium quantities
(such as 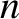 ,
, 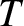 , and
, and 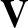 ). Demonstrate that it is a
good approximation to write
). Demonstrate that it is a
good approximation to write

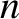 and
and 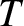 are uniform, but that
are uniform, but that
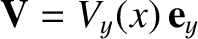 . Demonstrate that the only non-zero components of the viscosity
tensor are
. Demonstrate that the only non-zero components of the viscosity
tensor are
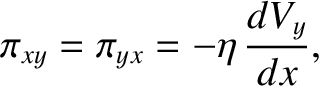
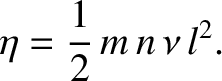
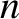 is uniform, and
is uniform, and
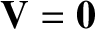 , but that
, but that 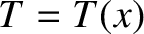 .
Demonstrate that the only non-zero component of the heat flux density is
.
Demonstrate that the only non-zero component of the heat flux density is
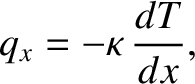
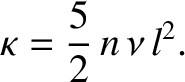
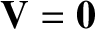 , and
, and 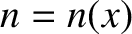 and
and 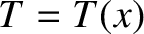 , but that
, but that 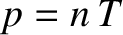 is constant.
Demonstrate that the only non-zero component of the heat flux density is
is constant.
Demonstrate that the only non-zero component of the heat flux density is
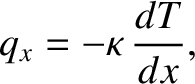

 and
and  be the electron number density and temperature, respectively. Let
be the electron number density and temperature, respectively. Let 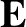 be the ambient electric field. The electron distribution
function
be the ambient electric field. The electron distribution
function 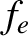 satisfies the simplified kinetic equation
satisfies the simplified kinetic equation
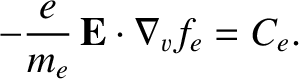
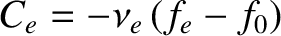
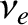 is the effective electron-ion collision frequency, and
is the effective electron-ion collision frequency, and
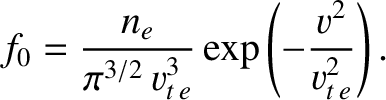
 . Suppose that
. Suppose that
 .
Demonstrate that it is a
good approximation to write
.
Demonstrate that it is a
good approximation to write