Next: Debye Shielding Up: Plasma Parameters Previous: Fundamental Parameters Contents
It is easily seen that  corresponds to the typical electrostatic
oscillation frequency of a given species in response to a small charge separation.
For instance, consider a one-dimensional situation in which a slab (whose bounding planes are normal to the
corresponds to the typical electrostatic
oscillation frequency of a given species in response to a small charge separation.
For instance, consider a one-dimensional situation in which a slab (whose bounding planes are normal to the 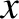 -axis)
consisting entirely of particles of one species (with charge
-axis)
consisting entirely of particles of one species (with charge 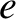 and mass
and mass 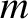 ) is displaced from its
quasi-neutral position by an infinitesimal distance
) is displaced from its
quasi-neutral position by an infinitesimal distance 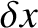 (parallel to the
(parallel to the 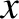 -axis). The
resulting charge density that develops on the leading face of the slab is
-axis). The
resulting charge density that develops on the leading face of the slab is
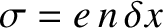 . An equal and opposite charge density develops on the
opposite face.
The
. An equal and opposite charge density develops on the
opposite face.
The 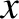 -directed electric field generated inside
the slab is
-directed electric field generated inside
the slab is
 (Fitzpatrick 2008).
Thus, Newton's second law of motion applied to an individual particle inside the slab yields
(Fitzpatrick 2008).
Thus, Newton's second law of motion applied to an individual particle inside the slab yields
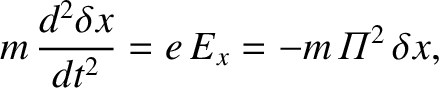 |
(1.6) |
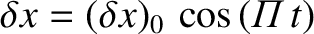 .
.
Plasma oscillations are observed only when the plasma system
is studied over time periods,  , longer than the plasma period,
, longer than the plasma period,
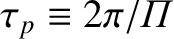 , and when external influences modify the system at
a rate no faster than
, and when external influences modify the system at
a rate no faster than  . In the opposite case, one is obviously studying
something other than plasma physics (for instance, nuclear reactions), and the
system cannot usefully be considered to be a plasma. Similarly, observations
over lengthscales
. In the opposite case, one is obviously studying
something other than plasma physics (for instance, nuclear reactions), and the
system cannot usefully be considered to be a plasma. Similarly, observations
over lengthscales  shorter than the distance
shorter than the distance
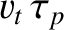 traveled
by a typical plasma particle during a plasma period will also not
detect plasma behavior. In this case, particles will exit the
system before completing a plasma oscillation. This distance, which is the
spatial equivalent to
traveled
by a typical plasma particle during a plasma period will also not
detect plasma behavior. In this case, particles will exit the
system before completing a plasma oscillation. This distance, which is the
spatial equivalent to  , is called the Debye length, and is defined
, is called the Debye length, and is defined
According to the preceding discussion, our idealized system can usefully be considered to be a plasma only if
and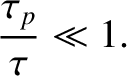 |
(1.10) |
 and
and 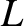 represent the typical timescale and lengthscale of the
process under investigation.
represent the typical timescale and lengthscale of the
process under investigation.
It should be noted that, despite the conventional requirement given in Equation (1.9), plasma physics is actually capable of describing structures on the Debye scale (Hazeltine and Waelbroeck 2004). The most important example of this ability is the theory of the Langmuir sheath, which is the boundary layer that surrounds a plasma confined by a material surface (Lieberman and Lichtenberg 2005). (See Section 4.17.)