Next: Drift Equations Up: Plasma Fluid Theory Previous: Cold-Plasma Equations Contents
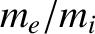 . Now, according to the ordering adopted in Section 4.12,
. Now, according to the ordering adopted in Section 4.12,
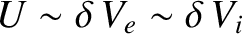 in the MHD limit. It follows from Equations (4.181) and (4.182)
that
in the MHD limit. It follows from Equations (4.181) and (4.182)
that
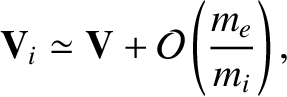 |
(4.192) |
![$\displaystyle {\bf V}_e \simeq {\bf V} - [\delta]\,\frac{{\bf j}}{n\,e} + {\cal O}\left(\frac{m_e}
{m_i}\right).$](img1489.png) |
(4.193) |
Equations (4.186) and (4.189) yield the continuity equation:
where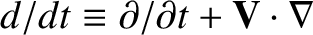 .
.
Equations (4.187) and (4.190) can be summed to give the equation of motion:
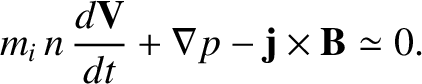 |
(4.195) |
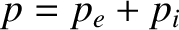 is the total pressure.
Note that all terms in the previous equation are the same order in
is the total pressure.
Note that all terms in the previous equation are the same order in 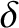 .
.
The
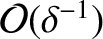 components of Equations (4.187) and (4.190) yield
the Ohm's law:
components of Equations (4.187) and (4.190) yield
the Ohm's law:
Equations (4.188) and (4.191) can be summed to give the energy evolution equation:
Equations (4.194) and (4.197) can be combined to give the more familiar adiabatic equation of state: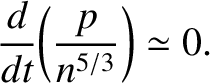 |
(4.198) |
Finally, the
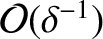 components of Equations (4.188) and (4.191)
yield
components of Equations (4.188) and (4.191)
yield
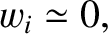 |
(4.199) |
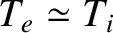 [see Equation (4.82)]. Thus, we expect equipartition of the
thermal energy between electrons and ions in the MHD limit.
[see Equation (4.82)]. Thus, we expect equipartition of the
thermal energy between electrons and ions in the MHD limit.