The fact that two-particle Coulomb collisions are dominated by small-angle scattering events allows some simplification of
the Boltzmann collision operator in a plasma.
According to Equations (3.26) and (3.70), the Boltzmann collision operator for
two-body Coulomb collisions between species- particles (with mass
particles (with mass 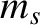 and charge
and charge 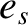 ) and species-
) and species- particles (with mass
particles (with mass 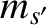 and charge
and charge 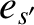 ) can be written
) can be written
 |
(3.71) |
where
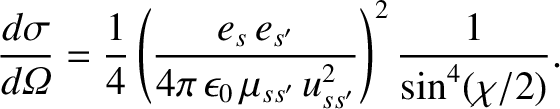 |
(3.72) |
Here,
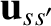 is the relative velocity prior to a collision, and
is the relative velocity prior to a collision, and
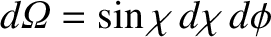 , where
, where 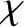 is the angle of deflection, and
is the angle of deflection, and
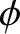 is an azimuthal angle that determines the orientation of the plane in which a given two-body collision occurs. Recall that
is an azimuthal angle that determines the orientation of the plane in which a given two-body collision occurs. Recall that  ,
, 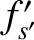 ,
, 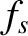 , and
, and 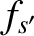 are short-hand for
are short-hand for
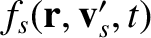 ,
,
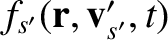 ,
,
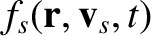 , and
, and
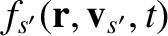 , respectively.
, respectively.
The species- and species-
and species- particle velocities prior to the collision are
particle velocities prior to the collision are 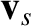 and
and
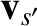 , respectively, so that
, respectively, so that
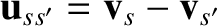 . Let us write the corresponding
velocities after the collision as (see Section 3.3)
. Let us write the corresponding
velocities after the collision as (see Section 3.3)
Here,
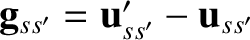 is assumed to be small, which implies that the angle of deflection is also small.
Expanding
is assumed to be small, which implies that the angle of deflection is also small.
Expanding
 to second order in
to second order in
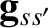 , we obtain
, we obtain
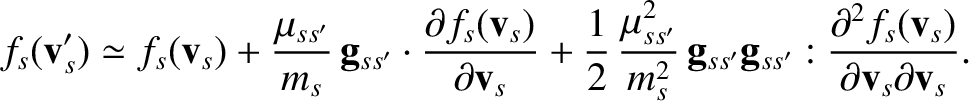 |
(3.75) |
Likewise, expanding
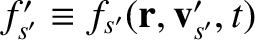 , we get
, we get
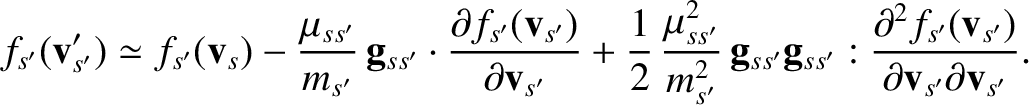 |
(3.76) |
Note that, in writing the previous two equations, we have neglected the 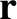 and
and 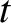 dependence of
dependence of
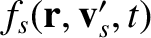 , et cetera, for ease of notation.
Hence,
It follows that
, et cetera, for ease of notation.
Hence,
It follows that
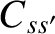 |
![$\displaystyle \simeq \frac{1}{4}\left(\frac{e_s\,e_{s'}}{4\pi\,\epsilon_0\,\mu_...
...}_{ss'}\right]\frac{d^3{\bf v}_{s'}\,d{\mit\Omega}}{u_{ss'}^3\,\sin^4(\chi/2)},$](img749.png) |
|
| |
|
(3.78) |
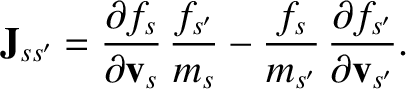 |
(3.79) |
Let  ,
, 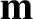 , and
, and 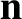 be a right-handed set of mutually orthogonal unit vectors. Suppose that
be a right-handed set of mutually orthogonal unit vectors. Suppose that
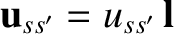 .
Recall that
.
Recall that
 . Now, in an elastic collision for which the angle of deviation is
. Now, in an elastic collision for which the angle of deviation is 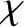 , we
require
, we
require
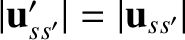 ,
,
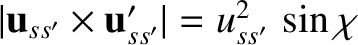 , and
, and
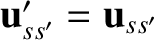 when
when 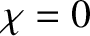 . In other words,
we need
. In other words,
we need
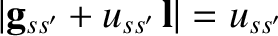 ,
,
 , and
, and
 when
when 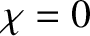 .
We deduce that
.
We deduce that
![$\displaystyle {\bf g}_{ss'} \simeq u_{ss'}\left[(\cos\chi-1)\,{\bf l} + \sin\chi\,\cos\phi\,{\bf m} +\sin\chi\,\sin\phi\,{\bf n}\right].$](img762.png) |
(3.80) |
Thus,
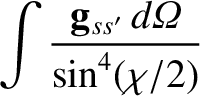 |
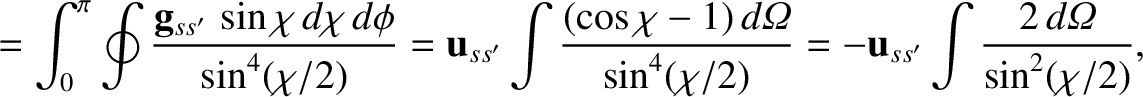 |
(3.81) |
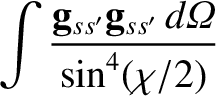 |
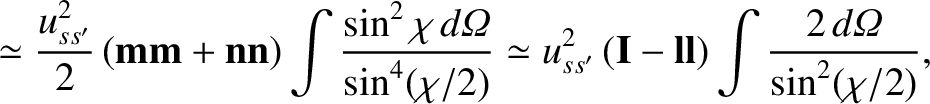 |
(3.82) |
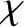 is small.
is small.
Now,
 |
(3.83) |
where
 and
and
 are the maximum and minimum angles of deflection, respectively.
However, according to Equation (3.64), small-angle two-body Coulomb collisions are characterized by
are the maximum and minimum angles of deflection, respectively.
However, according to Equation (3.64), small-angle two-body Coulomb collisions are characterized by
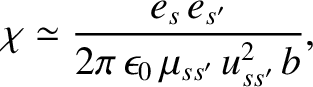 |
(3.84) |
where 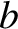 is the impact parameter. Thus, we can write
is the impact parameter. Thus, we can write
 |
(3.85) |
where the quantity
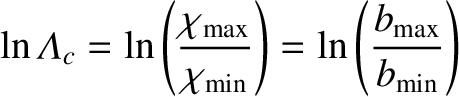 |
(3.86) |
is known as the Coulomb logarithm.
It follows from the previous analysis that
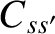 |
![$\displaystyle = \left(\frac{e_s\,e_{s'}}{4\pi\,\epsilon_0\,\mu_{ss'}}\right)^24...
...rac{\partial}{\partial {\bf v}_{s'}}\right){\bf J}_{ss'}\right]d^3{\bf v}_{s'}.$](img773.png) |
|
| |
|
(3.87) |
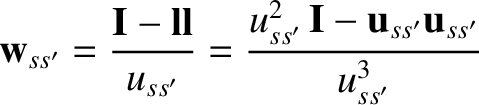 |
(3.88) |
then it is readily seen that
Here, 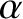 ,
, 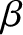 , and
, and 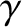 run from
run from 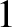 to
to 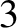 , and correspond to Cartesian components. Moreover, we have made use of the Einstein summation convention
(that repeated indices are implicitly summed from
, and correspond to Cartesian components. Moreover, we have made use of the Einstein summation convention
(that repeated indices are implicitly summed from 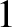 to
to 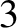 ) (Riley 1974).
Hence, we deduce that
) (Riley 1974).
Hence, we deduce that
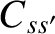 |
![$\displaystyle = \left(\frac{e_s\,e_{s'}}{4\pi\,\epsilon_0\,\mu_{ss'}}\right)^24...
...rac{\partial}{\partial {\bf v}_{s'}}\right){\bf J}_{ss'}\right]d^3{\bf v}_{s'}.$](img779.png) |
|
| |
|
(3.90) |
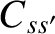 |
![$\displaystyle = \left(\frac{e_s\,e_{s'}}{4\pi\,\epsilon_0\,\mu_{ss'}}\right)^24...
...{\bf v}_{s'}}\cdot{\bf w}_{ss'}\right)\cdot{\bf J}_{ss'}\right]d^3{\bf v}_{s'}.$](img780.png) |
|
| |
|
(3.91) |
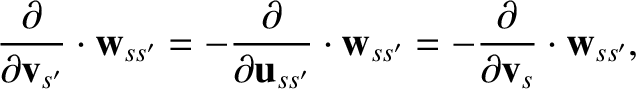 |
(3.92) |
because
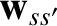 is a function of
is a function of
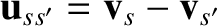 . Thus, we obtain the so-called Landau collision operator (Landau 1936),
. Thus, we obtain the so-called Landau collision operator (Landau 1936),
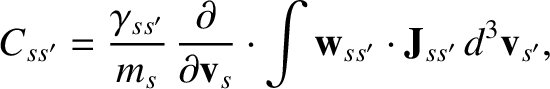 |
(3.93) |
where
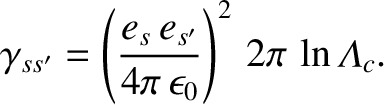 |
(3.94) |
 particles (with mass
particles (with mass 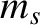 and charge
and charge 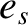 ) and species-
) and species- particles (with mass
particles (with mass 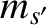 and charge
and charge 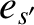 ) can be written
) can be written

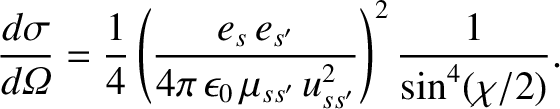
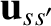 is the relative velocity prior to a collision, and
is the relative velocity prior to a collision, and
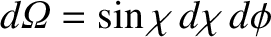 , where
, where 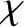 is the angle of deflection, and
is the angle of deflection, and
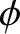 is an azimuthal angle that determines the orientation of the plane in which a given two-body collision occurs. Recall that
is an azimuthal angle that determines the orientation of the plane in which a given two-body collision occurs. Recall that  ,
, 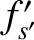 ,
, 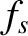 , and
, and 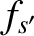 are short-hand for
are short-hand for
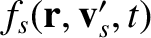 ,
,
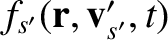 ,
,
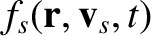 , and
, and
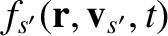 , respectively.
, respectively.
 and species-
and species- particle velocities prior to the collision are
particle velocities prior to the collision are 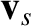 and
and
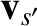 , respectively, so that
, respectively, so that
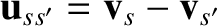 . Let us write the corresponding
velocities after the collision as (see Section 3.3)
. Let us write the corresponding
velocities after the collision as (see Section 3.3)

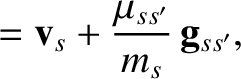
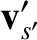
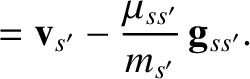
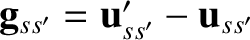 is assumed to be small, which implies that the angle of deflection is also small.
Expanding
is assumed to be small, which implies that the angle of deflection is also small.
Expanding
 to second order in
to second order in
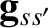 , we obtain
, we obtain
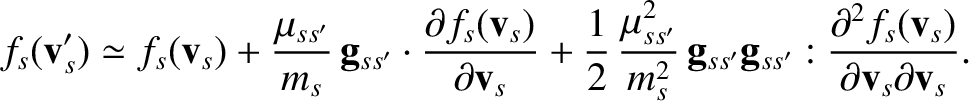
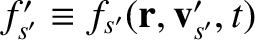 , we get
, we get
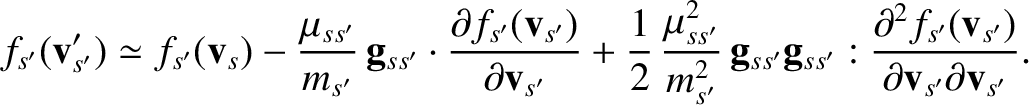
 and
and  dependence of
dependence of
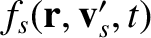 , et cetera, for ease of notation.
Hence,
, et cetera, for ease of notation.
Hence,
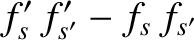
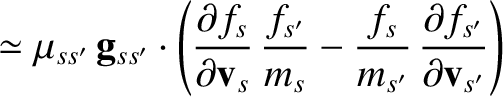
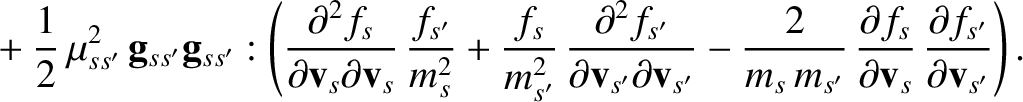
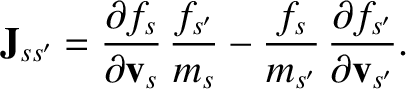
 ,
, 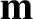 , and
, and 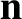 be a right-handed set of mutually orthogonal unit vectors. Suppose that
be a right-handed set of mutually orthogonal unit vectors. Suppose that
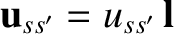 .
Recall that
.
Recall that
 . Now, in an elastic collision for which the angle of deviation is
. Now, in an elastic collision for which the angle of deviation is 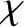 , we
require
, we
require
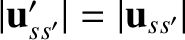 ,
,
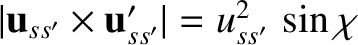 , and
, and
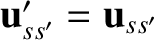 when
when 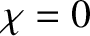 . In other words,
we need
. In other words,
we need
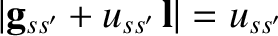 ,
,
 , and
, and
 when
when 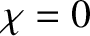 .
We deduce that
.
We deduce that
![$\displaystyle {\bf g}_{ss'} \simeq u_{ss'}\left[(\cos\chi-1)\,{\bf l} + \sin\chi\,\cos\phi\,{\bf m} +\sin\chi\,\sin\phi\,{\bf n}\right].$](img762.png)
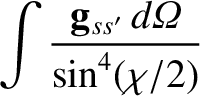
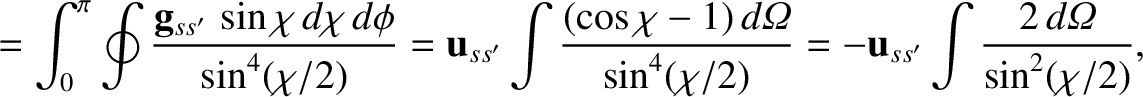
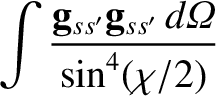
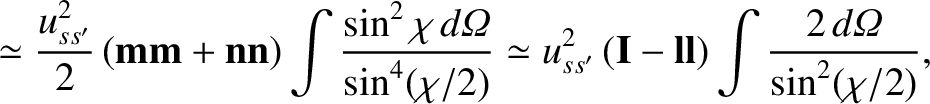
 is small.
is small.

 and
and
 are the maximum and minimum angles of deflection, respectively.
However, according to Equation (3.64), small-angle two-body Coulomb collisions are characterized by
where
are the maximum and minimum angles of deflection, respectively.
However, according to Equation (3.64), small-angle two-body Coulomb collisions are characterized by
where 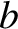 is the impact parameter. Thus, we can write
where the quantity
is known as the Coulomb logarithm.
is the impact parameter. Thus, we can write
where the quantity
is known as the Coulomb logarithm.
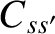
![$\displaystyle = \left(\frac{e_s\,e_{s'}}{4\pi\,\epsilon_0\,\mu_{ss'}}\right)^24...
...rac{\partial}{\partial {\bf v}_{s'}}\right){\bf J}_{ss'}\right]d^3{\bf v}_{s'}.$](img773.png)
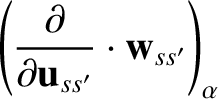
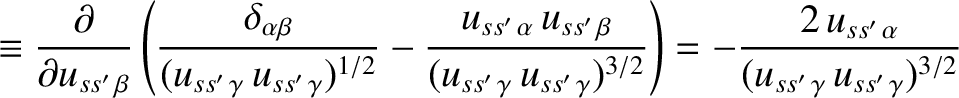
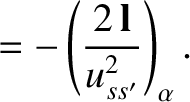
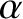 ,
, 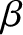 , and
, and 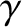 run from
run from 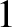 to
to 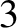 , and correspond to Cartesian components. Moreover, we have made use of the Einstein summation convention
(that repeated indices are implicitly summed from
, and correspond to Cartesian components. Moreover, we have made use of the Einstein summation convention
(that repeated indices are implicitly summed from 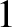 to
to 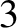 ) (Riley 1974).
Hence, we deduce that
) (Riley 1974).
Hence, we deduce that
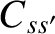
![$\displaystyle = \left(\frac{e_s\,e_{s'}}{4\pi\,\epsilon_0\,\mu_{ss'}}\right)^24...
...rac{\partial}{\partial {\bf v}_{s'}}\right){\bf J}_{ss'}\right]d^3{\bf v}_{s'}.$](img779.png)
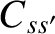
![$\displaystyle = \left(\frac{e_s\,e_{s'}}{4\pi\,\epsilon_0\,\mu_{ss'}}\right)^24...
...{\bf v}_{s'}}\cdot{\bf w}_{ss'}\right)\cdot{\bf J}_{ss'}\right]d^3{\bf v}_{s'}.$](img780.png)
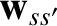 is a function of
is a function of
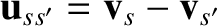 . Thus, we obtain the so-called Landau collision operator (Landau 1936),
where
. Thus, we obtain the so-called Landau collision operator (Landau 1936),
where