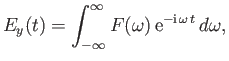 |
(6.70) |
The pulse structure is conveniently represented as
Each component frequency of the pulse yields a wave that
propagates independently along the ![]() -axis, in a manner specified by the
appropriate WKB solution [see Equations (6.17) and (6.18)]. Thus, if Equation (6.70)
specifies the signal at the antenna (i.e., at
-axis, in a manner specified by the
appropriate WKB solution [see Equations (6.17) and (6.18)]. Thus, if Equation (6.70)
specifies the signal at the antenna (i.e., at
![]() ) then the signal at coordinate
) then the signal at coordinate ![]() (where
(where
![]() )
is given by
)
is given by
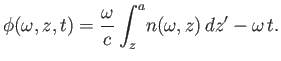 |
(6.72) |
Equation (6.71) can be regarded as a contour integral in ![]() -space.
The quantity
-space.
The quantity
![]() is a relatively slowly varying function of
is a relatively slowly varying function of
![]() , whereas the phase,
, whereas the phase, ![]() , is a large and rapidly varying
function of
, is a large and rapidly varying
function of ![]() .
The rapid
oscillations of
.
The rapid
oscillations of
![]() over most of the path of
integration ensure that the integrand averages almost to zero. However,
this cancellation argument does not apply to places on the
integration path where the phase
is stationary: that is,
places where
over most of the path of
integration ensure that the integrand averages almost to zero. However,
this cancellation argument does not apply to places on the
integration path where the phase
is stationary: that is,
places where
![]() has an extremum. The integral can, therefore, be
estimated by finding those points where
has an extremum. The integral can, therefore, be
estimated by finding those points where
![]() has a vanishing derivative,
evaluating (approximately) the integral in the neighborhood of each of
these points, and summing the contributions. This procedure is called
the method of stationary phase (Budden 1985).
has a vanishing derivative,
evaluating (approximately) the integral in the neighborhood of each of
these points, and summing the contributions. This procedure is called
the method of stationary phase (Budden 1985).
Suppose that
![]() has a vanishing first derivative
at
has a vanishing first derivative
at
![]() . In the neighborhood of this point,
. In the neighborhood of this point,
![]() can be expanded as a Taylor series,
can be expanded as a Taylor series,
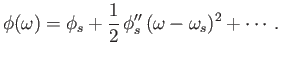 |
(6.73) |
![$\displaystyle E_{y\,s} \simeq \frac{F(\omega_s) \,{\rm e}^{\,{\rm i}\,\phi_s}}{...
...ty} \exp\left[\frac{\rm i}{2}\,\phi_s''\,(\omega-\omega_s)^{\,2}\right]d\omega.$](img2098.png) |
(6.74) |
![$\displaystyle E_{y\,s}\simeq \frac{F(\omega_s) \,{\rm e}^{\,{\rm i}\,\phi_s}}{n...
...left(\pi \,t^{\,2}/2\right)+{\rm i}\,\sin\left(\pi\, t^{\,2}/2\right)\right]dt,$](img2099.png) |
(6.75) |
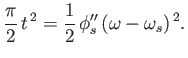 |
(6.76) |
 |
(6.77) |
Integrals of the form (6.71) can be calculated exactly using the
method of steepest descent (Brillouin 1960; Budden 1985). The stationary
phase approximation (6.78) agrees with the leading term of the
method of steepest descent (which is far more difficult to implement
than the method of stationary phase) provided that
![]() is
real (i.e., provided that
the stationary point lies on the real axis). If
is
real (i.e., provided that
the stationary point lies on the real axis). If ![]() is complex, however, then the stationary phase
method can yield erroneous results.
is complex, however, then the stationary phase
method can yield erroneous results.
It follows, from the previous discussion,
that the right-hand side of Equation (6.71) averages to a very small
value, expect
for those special values of ![]() and
and ![]() at which one of the points of stationary
phase in
at which one of the points of stationary
phase in ![]() -space coincides with one of the peaks of
-space coincides with one of the peaks of ![]() . The
locus of these special values of
. The
locus of these special values of ![]() and
and ![]() can obviously be regarded as the
equation of motion of the pulse as it propagates along the
can obviously be regarded as the
equation of motion of the pulse as it propagates along the ![]() -axis. Thus, the equation of motion is
specified by
-axis. Thus, the equation of motion is
specified by
 |
(6.79) |
Suppose that the ![]() -velocity of a pulse of central frequency
-velocity of a pulse of central frequency ![]() at coordinate
at coordinate ![]() is given by
is given by
![]() . The differential
equation of motion of the pulse is then
. The differential
equation of motion of the pulse is then
![]() . This can be integrated,
using the boundary condition
. This can be integrated,
using the boundary condition ![]() at
at ![]() , to give the full equation
of motion:
, to give the full equation
of motion:
The dispersion relation for an electromagnetic plasma wave propagating through an unmagnetized plasma is [see Equation (6.121)]
| (6.86) |
Although we have only analyzed the motion of the
pulse as it travels from the antenna to the reflection point, it is
easily demonstrated that the speed of the reflected pulse at position
![]() is the same as that of the incident pulse. In other words, the group velocities
of pulses traveling in opposite directions are of equal magnitude.
is the same as that of the incident pulse. In other words, the group velocities
of pulses traveling in opposite directions are of equal magnitude.