


Next: Plane Waves in Homogeneous
Up: Waves in Cold Plasmas
Previous: Waves in Cold Plasmas
The cold-plasma equations describe waves (and other perturbations) that
propagate through a plasma much faster than a typical thermal velocity. (See Section 4.11.)
The collective
motions described by the cold-plasma model are closely related to the individual particle motions
discussed in Chapter 2. In fact, in the
cold-plasma model, all particles (of a given species) at a given position effectively move with the
same velocity. It follows that the fluid velocity is identical to the particle
velocity, and is, therefore, governed by the same equations.
However, the cold-plasma
model goes beyond the single-particle description because it determines the
electromagnetic fields self-consistently in terms of the
charge and current densities generated by the particle motions. In this chapter, we shall use the cold-plasma equations to
investigate the properties of small amplitude plasma waves.
What role, if any, does the geometry of the plasma equilibrium play in
determining the properties of plasma waves? Clearly, geometry plays a
key role for modes whose wavelengths are comparable to the dimensions of
the plasma. However, it is plausible that waves whose wavelengths are
much
smaller than the plasma dimensions
have properties that are, in a local sense, independent of the
geometry. In other words, the local properties of small wavelength plasma oscillations are
universal in nature. To investigate these properties, we
can, to a first approximation, represent the plasma as a homogeneous
equilibrium (corresponding to the limit
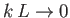 , where
, where 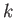 is the magnitude of the wavevector, and
is the magnitude of the wavevector, and 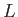 is the characteristic
equilibrium lengthscale).
is the characteristic
equilibrium lengthscale).



Next: Plane Waves in Homogeneous
Up: Waves in Cold Plasmas
Previous: Waves in Cold Plasmas
Richard Fitzpatrick
2016-01-23
![]() , where
, where ![]() is the magnitude of the wavevector, and
is the magnitude of the wavevector, and ![]() is the characteristic
equilibrium lengthscale).
is the characteristic
equilibrium lengthscale).