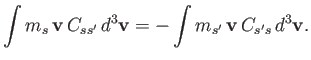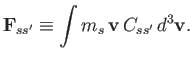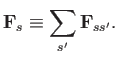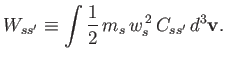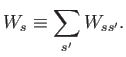Next: Moments of Kinetic Equation
Up: Plasma Fluid Theory
Previous: Moments of Distribution Function
Moments of Collision Operator
Boltzmann's collision operator for a neutral gas considers only
binary collisions, and is, therefore, bilinear in the distribution functions
of the two colliding species. (See Section 3.4.)
In other words,
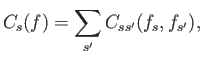 |
(4.19) |
where 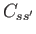 is linear in each of its arguments. Unfortunately, such bilinearity
is not strictly valid for the case of Coulomb collisions in a plasma.
Because of the long-range nature of the Coulomb interaction, the closest analogue
to ordinary two-particle interaction is modified by Debye shielding, which is an intrinsically
many-body effect. Fortunately, the departure from bilinearity is logarithmic
in a weakly coupled plasma, and can, therefore, be neglected to a fairly good approximation
(because a logarithm is a comparatively weakly varying function). (See Section 3.10.)
Thus, from now
on,
is linear in each of its arguments. Unfortunately, such bilinearity
is not strictly valid for the case of Coulomb collisions in a plasma.
Because of the long-range nature of the Coulomb interaction, the closest analogue
to ordinary two-particle interaction is modified by Debye shielding, which is an intrinsically
many-body effect. Fortunately, the departure from bilinearity is logarithmic
in a weakly coupled plasma, and can, therefore, be neglected to a fairly good approximation
(because a logarithm is a comparatively weakly varying function). (See Section 3.10.)
Thus, from now
on, 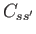 is presumed to be bilinear.
is presumed to be bilinear.
It is important to realize that there is no simple relationship between
the quantity
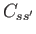 , which describes the effect on species
, which describes the effect on species 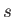 of
collisions with species
of
collisions with species 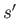 , and the quantity
, and the quantity 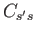 . The two operators
can have quite distinct mathematical forms (for example, where the masses
. The two operators
can have quite distinct mathematical forms (for example, where the masses
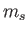 and
and 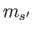 are significantly different), and they do not appear in the same equations.
are significantly different), and they do not appear in the same equations.
Neutral particle collisions are characterized by Boltzmann's collisional
conservation laws. (See Section 3.5.) In fact, the collisional process conserves particles, momentum,
and energy at each point in space. We expect the same local conservation
laws to hold for Coulomb collisions in a plasma, because the maximum range of the
Coulomb force in a plasma is the Debye length, which is assumed to
be vanishingly small.
Collisional particle conservation is expressed as
 |
(4.20) |
Collisional momentum conservation requires that
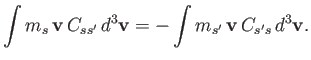 |
(4.21) |
In other words, there is zero net momentum exchanged between species 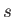 and
and 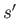 .
It is useful to introduce the rate of collisional momentum exchange, which is called the
collisional friction force, or simply the friction force:
.
It is useful to introduce the rate of collisional momentum exchange, which is called the
collisional friction force, or simply the friction force:
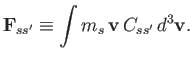 |
(4.22) |
Clearly,
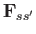 is the momentum-moment of the collision operator.
The total friction force experienced by species
is the momentum-moment of the collision operator.
The total friction force experienced by species 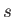 is
is
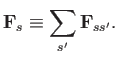 |
(4.23) |
Momentum conservation is expressed in detailed form as
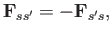 |
(4.24) |
and in non-detailed form as
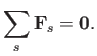 |
(4.25) |
Collisional energy conservation requires the quantity
 |
(4.26) |
to be conserved in collisions. In other words,
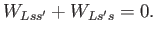 |
(4.27) |
Here, the 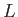 -subscript indicates that the kinetic energy of both
species is measured in the same laboratory frame. Because of Galilean invariance,
the choice of this common reference frame does not matter.
-subscript indicates that the kinetic energy of both
species is measured in the same laboratory frame. Because of Galilean invariance,
the choice of this common reference frame does not matter.
An alternative collisional energy-moment is
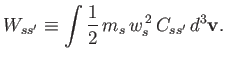 |
(4.28) |
This is the kinetic energy change experienced by species 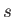 , due to
collisions with species
, due to
collisions with species 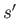 , measured in the rest frame of species
, measured in the rest frame of species 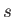 .
The total energy change for species
.
The total energy change for species 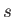 is
is
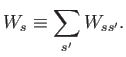 |
(4.29) |
It is easily verified that
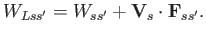 |
(4.30) |
Thus, the collisional energy conservation law can be written in detailed form as
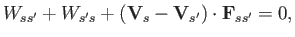 |
(4.31) |
or in non-detailed form as
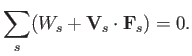 |
(4.32) |



Next: Moments of Kinetic Equation
Up: Plasma Fluid Theory
Previous: Moments of Distribution Function
Richard Fitzpatrick
2016-01-23
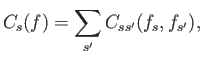
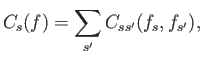
![]() , which describes the effect on species
, which describes the effect on species ![]() of
collisions with species
of
collisions with species ![]() , and the quantity
, and the quantity ![]() . The two operators
can have quite distinct mathematical forms (for example, where the masses
. The two operators
can have quite distinct mathematical forms (for example, where the masses
![]() and
and ![]() are significantly different), and they do not appear in the same equations.
are significantly different), and they do not appear in the same equations.