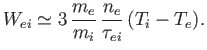![$\displaystyle f ({\bf v})= n\left(\frac{m}{2\pi\,T}\right)^{3/2}\,\exp\left[-\frac{m\,({\bf v}-{\bf V})^{\,2}}{2\,T}\right].
$](img973.png)
Demonstrate that
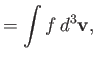 |
||
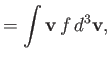 |
||
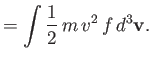 |
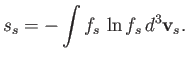
The Boltzmann H-theorem thus states that collisions drive the system toward a maximum entropy state characterized by Maxwellian distribution functions with common mean velocities and common temperatures. Demonstrate that for a Maxwellian distribution,
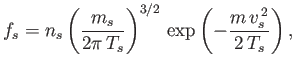
the entropy per unit volume takes the form
![$\displaystyle s_s= n_s\left[\ln\left(\frac{T_s^{\,3/2}}{n_s}\right) +\frac{3}{2}\ln\left(\frac{2\pi}{m_s}\right)+\frac{3}{2}\right].
$](img982.png)
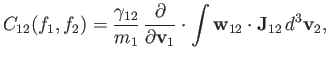
where
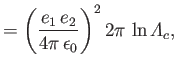 |
||
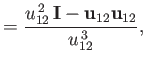 |
||
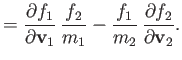 |
Demonstrate directly that this collision operator satisfies the same conservation laws as the Boltzmann collision operator. Namely,
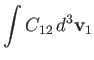 |
||
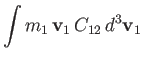 |
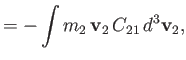 |
|
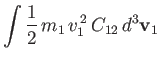 |
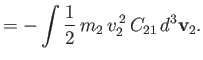 |
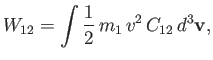
where
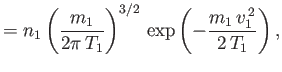 |
||
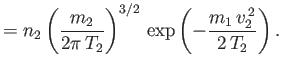 |
Suppose, further, that the kinetic temperatures of the two species are almost the same (i.e.,
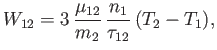
where the collision time,