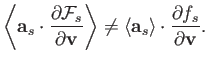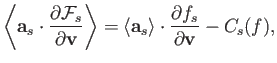Next: Two-Body Elastic Collisions
Up: Collisions
Previous: Introduction
Collision Operator
Plasma physics can be regarded formally as a closure of Maxwell's equations
by means of constitutive relations: that is, expressions
specifying the charge density, 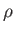 , and the current density,
, and the current density, 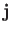 , in terms of
the electric and magnetic fields,
, in terms of
the electric and magnetic fields, 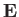 and
and 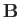 (Hazeltine and Waelbroeck 2004). Such relations can be expressed in terms of the microscopic distribution functions,
(Hazeltine and Waelbroeck 2004). Such relations can be expressed in terms of the microscopic distribution functions,
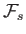 , for each plasma species:
, for each plasma species:
Here,
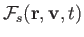 is the exact microscopic phase-space
density of plasma species
is the exact microscopic phase-space
density of plasma species 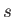 (with charge
(with charge 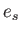 and mass
and mass 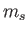 ) near
point
) near
point
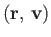 at time
at time 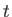 (Reif 1965). The distribution
function
(Reif 1965). The distribution
function
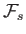 is normalized such that its velocity integral is equal to the
particle number density in coordinate space. In other words,
is normalized such that its velocity integral is equal to the
particle number density in coordinate space. In other words,
 |
(3.3) |
where
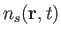 is the number (per unit volume) of species-
is the number (per unit volume) of species-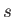 particles
near point
particles
near point  at time
at time 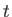 .
.
If we could determine each
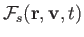 in terms of the
electromagnetic fields then Equations (3.1) and (3.2) would give us the
desired constitutive relations. In fact, the time evolution of the various distribution functions is determined
by particle conservation in phase-space, which requires that (Reif 1965)
in terms of the
electromagnetic fields then Equations (3.1) and (3.2) would give us the
desired constitutive relations. In fact, the time evolution of the various distribution functions is determined
by particle conservation in phase-space, which requires that (Reif 1965)
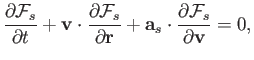 |
(3.4) |
where
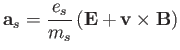 |
(3.5) |
is the species-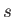 particle acceleration under the influence of the
particle acceleration under the influence of the 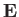 and
and
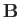 fields.
fields.
Equation (3.4) is easy to derive because it is exact, taking into
account all lengthscales from the microscopic to the macroscopic. Note, in
particular, that there is no statistical averaging involved in Equation (3.4).
It follows that the microscopic distribution function,
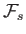 , is
essentially a sum of Dirac delta-functions, each following the
detailed trajectory of a single particle. Consequently, the electromagnetic
fields appearing in Equation (3.4) are extremely spiky on microscopic scales. In fact, solving Equation (3.4) is equivalent to solving the classical
electromagnetic many-body problem, which is a completely hopeless task.
, is
essentially a sum of Dirac delta-functions, each following the
detailed trajectory of a single particle. Consequently, the electromagnetic
fields appearing in Equation (3.4) are extremely spiky on microscopic scales. In fact, solving Equation (3.4) is equivalent to solving the classical
electromagnetic many-body problem, which is a completely hopeless task.
A much more useful equation can be extracted from Equation (3.4)
by ensemble averaging (Reif 1965). The average distribution function,
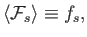 |
(3.6) |
is smooth on microscopic lengthscales, and is closely related to actual experimental measurements. Here, angle brackets denote
an ensemble average.
Similarly, the ensemble-averaged electromagnetic fields are also smooth.
Unfortunately, the extraction of an ensemble-averaged
equation from Equation (3.4) is mathematically challenging, and invariably
involves some level of approximation. The problem is that, because the
exact electromagnetic fields depend on particle trajectories, 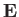 and
and
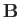 are not statistically independent of
are not statistically independent of
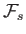 . In other
words, as a consequence of correlations between the distribution function and the electromagnetic fields on microscopic lengthscales,
the ensemble average of the nonlinear acceleration term in Equation (3.4) is such that
. In other
words, as a consequence of correlations between the distribution function and the electromagnetic fields on microscopic lengthscales,
the ensemble average of the nonlinear acceleration term in Equation (3.4) is such that
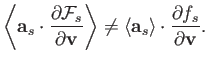 |
(3.7) |
It is convenient to write
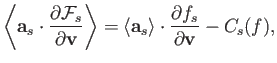 |
(3.8) |
where 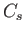 is an operator that
accounts for the correlations. Because the most important correlations result from
close encounters between particles,
is an operator that
accounts for the correlations. Because the most important correlations result from
close encounters between particles, 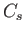 is known as the collision operator
(for species
is known as the collision operator
(for species 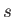 ).
It is not generally a linear operator, and usually involves the distribution
functions of both colliding species (the subscript in the
argument of
).
It is not generally a linear operator, and usually involves the distribution
functions of both colliding species (the subscript in the
argument of 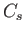 is omitted for this reason). Hence, the ensemble-averaged
version of Equation (3.4) is written
is omitted for this reason). Hence, the ensemble-averaged
version of Equation (3.4) is written
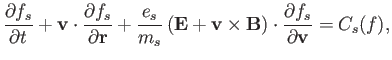 |
(3.9) |
where 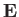 and
and 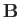 are now understood to be the smooth, ensemble-averaged electromagnetic fields.
Of course, in a weakly coupled plasma, the dominant collisions are two-particle Coulomb collisions.
Equation (3.9) is generally known as the kinetic equation.
are now understood to be the smooth, ensemble-averaged electromagnetic fields.
Of course, in a weakly coupled plasma, the dominant collisions are two-particle Coulomb collisions.
Equation (3.9) is generally known as the kinetic equation.



Next: Two-Body Elastic Collisions
Up: Collisions
Previous: Introduction
Richard Fitzpatrick
2016-01-23
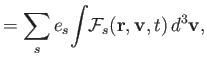
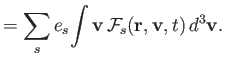

![]() in terms of the
electromagnetic fields then Equations (3.1) and (3.2) would give us the
desired constitutive relations. In fact, the time evolution of the various distribution functions is determined
by particle conservation in phase-space, which requires that (Reif 1965)
in terms of the
electromagnetic fields then Equations (3.1) and (3.2) would give us the
desired constitutive relations. In fact, the time evolution of the various distribution functions is determined
by particle conservation in phase-space, which requires that (Reif 1965)
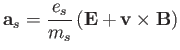
![]() , is
essentially a sum of Dirac delta-functions, each following the
detailed trajectory of a single particle. Consequently, the electromagnetic
fields appearing in Equation (3.4) are extremely spiky on microscopic scales. In fact, solving Equation (3.4) is equivalent to solving the classical
electromagnetic many-body problem, which is a completely hopeless task.
, is
essentially a sum of Dirac delta-functions, each following the
detailed trajectory of a single particle. Consequently, the electromagnetic
fields appearing in Equation (3.4) are extremely spiky on microscopic scales. In fact, solving Equation (3.4) is equivalent to solving the classical
electromagnetic many-body problem, which is a completely hopeless task.