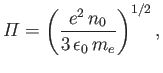Next: Charged Particle Motion
Up: Introduction
Previous: De Broglie Wavelength
- Consider a quasi-neutral plasma consisting of electrons of mass
 , charge
, charge 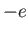 , temperature
, temperature 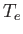 , and mean number density,
, and mean number density,  , as
well as ions of mass
, as
well as ions of mass  , charge
, charge 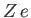 , temperature
, temperature  , and mean number density
, and mean number density 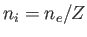 .
.
- Generalize the analysis of Section 1.4 to show that the effective plasma frequency of the
plasma can be written
where
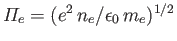 and
and
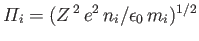 . Furthermore, demonstrate that
the characteristic ratio of ion to electron displacement in a plasma oscillation is
. Furthermore, demonstrate that
the characteristic ratio of ion to electron displacement in a plasma oscillation is
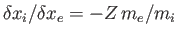 .
.
- Generalize the analysis of Section 1.5
to show that the effective Debye length,
 , of the plasma can be written
, of the plasma can be written
where
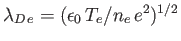 and
and
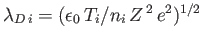 .
.
- The perturbed electrostatic potential
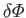 due to a charge
due to a charge 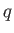 placed at the origin in
a plasma of Debye length
placed at the origin in
a plasma of Debye length  is governed by
is governed by
Show that the non-homogeneous solution to this equation
is
Demonstrate that the charge density of the shielding cloud is
and that the net shielding charge contained within a sphere of radius  , centered on the origin, is
, centered on the origin, is
- A quasi-neutral slab of cold (i.e.,
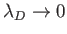 ) plasma whose bounding surfaces are normal to the
) plasma whose bounding surfaces are normal to the 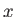 -axis consists of electrons of mass
-axis consists of electrons of mass  , charge
, charge 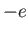 , and
mean number density
, and
mean number density  , as well as ions of charge
, as well as ions of charge 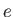 , and mean number density
, and mean number density  . The ions can effectively be treated as stationary. The slab is placed in an externally generated,
. The ions can effectively be treated as stationary. The slab is placed in an externally generated, 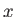 -directed
electric field that oscillates sinusoidally at the angular frequency
-directed
electric field that oscillates sinusoidally at the angular frequency 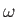 . By generalizing the analysis of Section 1.4, show
that the relative dielectric constant of the plasma is
. By generalizing the analysis of Section 1.4, show
that the relative dielectric constant of the plasma is
where
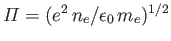 .
.
- A capacitor consists of two parallel plates of cross-sectional area
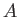 and spacing
and spacing
 . The region between the
capacitors is filled with a uniform hot plasma of Deybe length
. The region between the
capacitors is filled with a uniform hot plasma of Deybe length  . By generalizing the analysis of Section 1.5, show that the d.c. capacitance of the device is
. By generalizing the analysis of Section 1.5, show that the d.c. capacitance of the device is
- A uniform isothermal quasi-neutral plasma with singly-charged ions is placed in a relatively weak gravitational field of acceleration
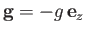 . Assuming,
first, that both species are distributed according to the Maxwell-Boltzmann statistics; second, that the perturbed electrostatic potential is a function of
. Assuming,
first, that both species are distributed according to the Maxwell-Boltzmann statistics; second, that the perturbed electrostatic potential is a function of
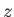 only; and, third, that the electric field is zero at
only; and, third, that the electric field is zero at  (and well behaved as
(and well behaved as
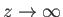 ), demonstrate that the electric field in the region
), demonstrate that the electric field in the region 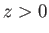 takes the form
takes the form
 ,
where
,
where
and
Here,  is the Debye length,
is the Debye length, 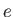 the magnitude of the electron charge, and
the magnitude of the electron charge, and  the ion mass.
the ion mass.
- Consider a charge sheet of charge density
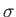 immersed in
a plasma of unperturbed particle number density
immersed in
a plasma of unperturbed particle number density  , ion temperature
, ion temperature
 , and electron temperature
, and electron temperature 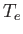 . Suppose that the charge sheet
coincides with the
. Suppose that the charge sheet
coincides with the 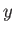 -
-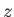 plane. Assuming that the (singly-charged) ions and electrons
obey Maxwell-Boltzmann statistics, demonstrate that in the limit
plane. Assuming that the (singly-charged) ions and electrons
obey Maxwell-Boltzmann statistics, demonstrate that in the limit
 the electrostatic
potential takes the form
the electrostatic
potential takes the form
where
![$ \lambda_D =[(\epsilon_0/e^2\,n_0)\,T_i\,T_e/(T_i+T_e)]^{1/2}$](img173.png) .
.
- Consider the previous exercise again. Let
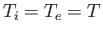 . Suppose, however,
that
. Suppose, however,
that
 is not necessarily much less than unity.
Demonstrate that the potential,
is not necessarily much less than unity.
Demonstrate that the potential, 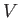 , of the charge sheet (relative to infinity)
satisfies
, of the charge sheet (relative to infinity)
satisfies
Furthermore, show that
where
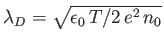 .
Let
.
Let 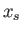 be the distance from the sheet at which the potential
has fallen to
be the distance from the sheet at which the potential
has fallen to 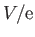 , where
, where
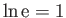 . Sketch
. Sketch
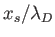 versus
versus 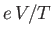 .
.
- A long cylinder of plasma of radius
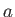 consists of cold (i.e.,
consists of cold (i.e.,  ) singly-charged ions and electrons with uniform number
density
) singly-charged ions and electrons with uniform number
density  . The cylinder of electrons is perturbed a distance
. The cylinder of electrons is perturbed a distance 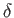 (where
(where
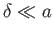 ) in a direction perpendicular to its axis.
) in a direction perpendicular to its axis.
- Assuming that the ions are immobile, show that the oscillation frequency of the electron
cylinder is
where  is the electron mass.
is the electron mass.
- Assuming that the ions have the finite mass
 , show that the oscillation frequency is
, show that the oscillation frequency is
- A sphere of plasma of radius
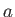 consists of cold (i.e.,
consists of cold (i.e.,  ) singly-charged ions and electrons with uniform number
density
) singly-charged ions and electrons with uniform number
density  . The sphere of electrons is perturbed a distance
. The sphere of electrons is perturbed a distance 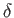 (where
(where
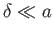 ).
Assuming that the ions are immobile, show that the oscillation frequency of the electron
sphere is
).
Assuming that the ions are immobile, show that the oscillation frequency of the electron
sphere is
where  is the electron mass.
is the electron mass.



Next: Charged Particle Motion
Up: Introduction
Previous: De Broglie Wavelength
Richard Fitzpatrick
2016-01-23
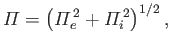
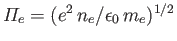 and
and
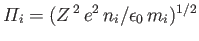 . Furthermore, demonstrate that
the characteristic ratio of ion to electron displacement in a plasma oscillation is
. Furthermore, demonstrate that
the characteristic ratio of ion to electron displacement in a plasma oscillation is
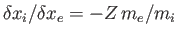 .
.
 , of the plasma can be written
, of the plasma can be written
![$\displaystyle \left(\frac{1}{\lambda_D}\right)^2 = \frac{1}{2}\left[\left(\frac{1}{\lambda_{D\,e}}\right)^2+ \left(\frac{1}{\lambda_{D\,i}}\right)^2\right],
$](img147.png)
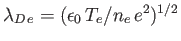 and
and
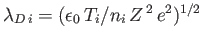 .
.
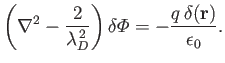
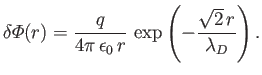
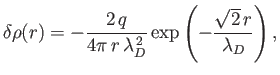
![$\displaystyle Q(r) = -q\left[1-\left(1+\frac{\sqrt{2}\,r}{\lambda_D}\right)\exp\left(-\frac{\sqrt{2}\,r}{\lambda_D}\right)\right].
$](img154.png)

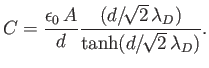
![$\displaystyle E_z(z) = E_0\left[1-\exp\left(\frac{\sqrt{2}\,z}{\lambda_D}\right)\right],
$](img167.png)
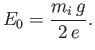
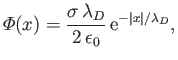
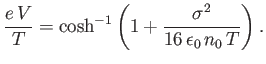

 is the electron mass.
is the electron mass.
 , show that the oscillation frequency is
, show that the oscillation frequency is
![$\displaystyle {\mit\Pi}=\left[\frac{e^2\,n_0}{2\,\epsilon_0}\left(\frac{1}{m_e}+\frac{1}{m_i}\right)\right]^{1/2}.
$](img189.png)