


Next: Velocity-Space Instabilities
Up: Waves in Warm Plasmas
Previous: Perpendicular Wave Propagation
It is instructive to consider the propagation of electrostatic waves through a magnetized plasma. Such
waves have purely electrostatic perturbed electric fields of the form
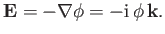 |
(8.114) |
Equation (8.8) can be generalized to give
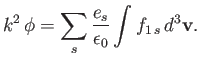 |
(8.115) |
Moreover, it follows from Equation (8.71) that
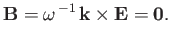 |
(8.116) |
In other words, there is no perturbed magnetic field associated with an electrostatic wave.
Equation (8.69) yields
Here,
 and
and
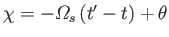 , whereas the Cartesian components of
, whereas the Cartesian components of  and
and 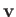 are written
are written
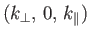 and
and
 , respectively. The equilibrium magnetic field takes the form
, respectively. The equilibrium magnetic field takes the form
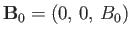 . Equations (8.115) and (8.117) can be
combined to give
. Equations (8.115) and (8.117) can be
combined to give
After some tedious analysis, the previous expression reduces to the so-called Harris dispersion relation (Harris 1961)
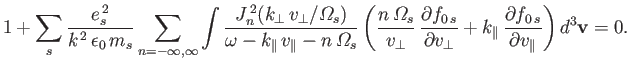 |
(8.119) |
For Maxwellian distribution functions of the form (8.79), we can explicitly perform the velocity-space integrals in the
Harris dispersion relation to give
![$\displaystyle 1+\sum_s\frac{2\,{\mit\Pi}_s^{\,2}}{(k_\parallel^{\,2} + k_\perp^...
...{\rm e}^{-\lambda_s}\!\sum_{n=-\infty,\infty}I_n(\lambda_s)\,Z(\xi_n)\right]=0,$](img3309.png) |
(8.120) |
where
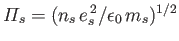 ,
,
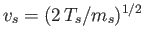 ,
,
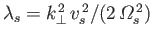 ,
and
,
and
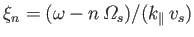 . Here, the
. Here, the 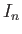 are modified Bessel functions (Abramowitz and Stegun 1965c), whereas
are modified Bessel functions (Abramowitz and Stegun 1965c), whereas
 is a plasma dispersion function. (See Section 8.4.) In deriving the previous expression, use has been made of the identity (Watson 1995)
is a plasma dispersion function. (See Section 8.4.) In deriving the previous expression, use has been made of the identity (Watson 1995)
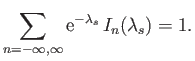 |
(8.121) |
Consider electrostatic waves propagating parallel to the equilibrium magnetic field. In this case,
 and
and
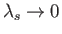 ,
so the dispersion relation (8.120) reduces to
,
so the dispersion relation (8.120) reduces to
![$\displaystyle 1 + \sum_s\frac{2\,{\mit\Pi}_s^{\,2}}{(k_\parallel\,v_s)^2}\left[1+\xi_0\,Z(\xi_0)\right]=0,$](img3313.png) |
(8.122) |
with the eigenvector
 . (Recall that
. (Recall that
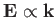 for an electrostatic wave.) It can be seen that this expression is identical to the
dispersion relation (8.97) for longitudinal plasma waves. Consider electrostatic waves propagating perpendicular to the equilibrium
magnetic field. In this case,
for an electrostatic wave.) It can be seen that this expression is identical to the
dispersion relation (8.97) for longitudinal plasma waves. Consider electrostatic waves propagating perpendicular to the equilibrium
magnetic field. In this case,
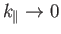 and
and
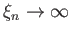 , so the dispersion relation (8.120) reduces to
, so the dispersion relation (8.120) reduces to
![$\displaystyle 1+\sum_s \frac{2\,{\mit\Pi}_s^{\,2}}{(k_\perp\,v_s)^2}\left[1-\xi...
... e}^{-\lambda_s}\!\sum_{n=-\infty,\infty}\frac{I_n(\lambda_s)}{\xi_n}\right]=0,$](img3314.png) |
(8.123) |
with the eigenvector
 . Making use of the identity (8.121), as well as the fact that
. Making use of the identity (8.121), as well as the fact that
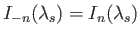 (Abramowitz and Stegun 1965c), the previous expression can be rearranged to give
(Abramowitz and Stegun 1965c), the previous expression can be rearranged to give
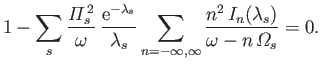 |
(8.124) |
It can be seen that this expression is identical to the dispersion relation (8.111) for Bernstein waves. Thus, we can now appreciate that plasma waves and
Bernstein waves are merely different aspects of a more general type of electrostatic wave. This wave takes the form of a plasma wave when propagating
parallel to the equilibrium magnetic field, of a Bernstein wave when propagating perpendicular to the magnetic field, and takes an intermediate form
when propagating obliquely to the magnetic field.



Next: Velocity-Space Instabilities
Up: Waves in Warm Plasmas
Previous: Perpendicular Wave Propagation
Richard Fitzpatrick
2016-01-23
![]() and
and
![]() ,
so the dispersion relation (8.120) reduces to
,
so the dispersion relation (8.120) reduces to
![$\displaystyle 1 + \sum_s\frac{2\,{\mit\Pi}_s^{\,2}}{(k_\parallel\,v_s)^2}\left[1+\xi_0\,Z(\xi_0)\right]=0,$](img3313.png)