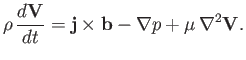
Likewise, we can add finite conductivity effects to the Ohm's law by including the term
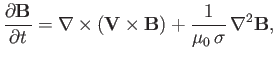
Show that the modified dispersion relation for Alfvén waves can be obtained from the standard one by multiplying both
and
If the finite conductivity and viscous corrections are small (i.e.,
![]() and
and
![]() ), show that, for
parallel (
), show that, for
parallel (![]() ) propagation, the
dispersion relation for the shear-Alfvén wave reduces to
) propagation, the
dispersion relation for the shear-Alfvén wave reduces to
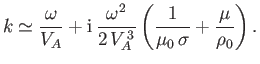
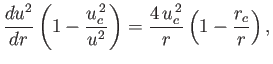
Show that this expression can be integrated to give
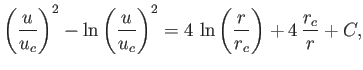
where
Let
![]() . Demonstrate that, in the limit
. Demonstrate that, in the limit ![]() , the previous expression yields either
, the previous expression yields either
or
![$\displaystyle u^2 = u_0^{\,2}\left[1+\frac{2\,u_c^{\,2}\,x^2}{u_0^{\,2}-u_c^{\,2}} + {\cal O}(x^3)\right],
$](img2966.png)
where
respectively, where
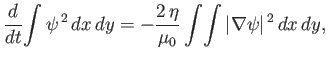
where
Given that
![]() , show that
, show that
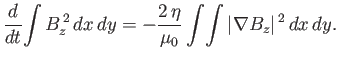
Hence, deduce that a two-dimensional ``axial'' magnetic field,
![$\displaystyle F(\bar{x}) = \left\{\begin{array}{lcl}
F'(0)\,\bar{x}&\mbox{\hspa...
... [0.5ex]
F'(0)\,{\rm sgn}(\bar{x})&&\vert\bar{x}\vert\geq 1\end{array}\right..
$](img2984.png)
This configuration is generated by a uniform,
![$\displaystyle {\mit\Delta}' = \frac{2\,\bar{k}}{\tanh(\bar{k})}\left[\frac{\bar{k} + \bar{k}\,\tanh(\bar{k})-1}{1-\bar{k}/\tanh(\bar{k})-\bar{k}}\right].
$](img2986.png)
Show that
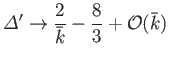
as
![$\displaystyle {\mit\Delta}'\rightarrow -2\,\bar{k} + 2\left[1+\frac{1}{2\,\bar{k}}+{\cal O}\left(\frac{1}{\bar{k}^{\,2}}\right)\right]\exp(-2\,\bar{k})
$](img2989.png)
as
Show that

where
- Show that, in this case, Equations (7.177) and (7.178) generalize to give
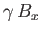
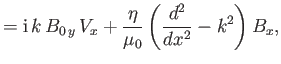
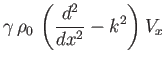
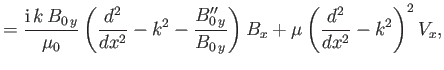
respectively. - Show that Equations (7.182) and (7.183) generalize to give
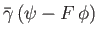
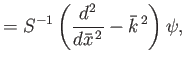
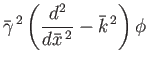

where
is the magnetic Prandtl number, and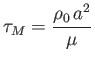
is the viscous diffusion time. - Show that the resistive layer equations, (7.187) and (7.188), generalize to give
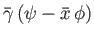
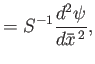
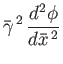
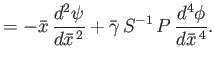
- Show that the Fourier transformed resistive layer equation, (7.196), generalizes to give
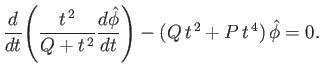
- Finally, solve the Fourier transformed resistive layer equation to determine the layer matching
parameter,
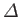 . Demonstrate that if
. Demonstrate that if
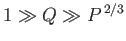 then
then
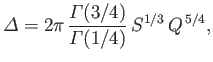
whereas if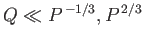 then
then
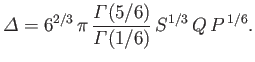
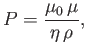
where
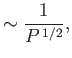 |
||
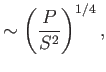 |
||
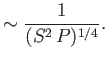 |
![$\displaystyle M_2 = \left[\frac{2+({\mit\Gamma}-1)\,M_1^{\,2}}{2\,{\mit\Gamma}\,M_1^{\,2} - ({\mit\Gamma}-1)}\right]^{1/2}.
$](img3014.png)
Hence, deduce that if
Hence, deduce that if the second law of thermodynamics requires the positive root of this equation to be such that
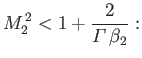
that is,
where