


Next: Boundary Value Problems with
Up: Electrostatics in Dielectric Media
Previous: Polarization
If the region in the vicinity of a collection of free charges contains dielectric material
of non-uniform dielectric constant then the electric field no longer
has the same form as in a vacuum. Suppose, for example, that
space is occupied by two dielectric media whose uniform dielectric
constants are
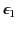 and
and
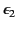 . What are the matching
conditions on
. What are the matching
conditions on 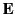 and
and 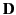 at the interface between the
two media?
at the interface between the
two media?
Imagine a Gaussian pill-box enclosing part of the interface. The thickness of the pill-box
is allowed to tend towards zero, so that the only contribution to
the outward flux of 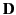 comes from its two flat faces. These faces
are parallel to the interface, and lie in each of the two
media. Their outward normals are
comes from its two flat faces. These faces
are parallel to the interface, and lie in each of the two
media. Their outward normals are
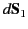 (in medium 1) and
(in medium 1) and
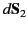 , where
, where
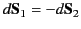 . Assuming that there
is no free charge inside the pill-box (which is reasonable in the limit
that the volume of the box tends towards zero), Equation (503)
yields
. Assuming that there
is no free charge inside the pill-box (which is reasonable in the limit
that the volume of the box tends towards zero), Equation (503)
yields
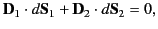 |
(508) |
where 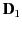 is the electric displacement in medium 1 at the
interface with medium 2, et cetera. The above equation can
be rewritten
is the electric displacement in medium 1 at the
interface with medium 2, et cetera. The above equation can
be rewritten
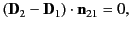 |
(509) |
where
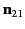 is the normal to the interface, directed from
medium 1 to medium 2.
If the fields and charges are non-time-varying then Maxwell's
equations yield
is the normal to the interface, directed from
medium 1 to medium 2.
If the fields and charges are non-time-varying then Maxwell's
equations yield
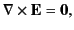 |
(510) |
which gives the
familiar boundary condition (obtained by integrating around a
small loop that straddles the interface)
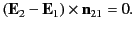 |
(511) |
In other word, the normal component of the electric displacement, and
the tangential component of the electric field, are both continuous across
any interface between two dielectric media.



Next: Boundary Value Problems with
Up: Electrostatics in Dielectric Media
Previous: Polarization
Richard Fitzpatrick
2014-06-27
![]() comes from its two flat faces. These faces
are parallel to the interface, and lie in each of the two
media. Their outward normals are
comes from its two flat faces. These faces
are parallel to the interface, and lie in each of the two
media. Their outward normals are
![]() (in medium 1) and
(in medium 1) and
![]() , where
, where
![]() . Assuming that there
is no free charge inside the pill-box (which is reasonable in the limit
that the volume of the box tends towards zero), Equation (503)
yields
. Assuming that there
is no free charge inside the pill-box (which is reasonable in the limit
that the volume of the box tends towards zero), Equation (503)
yields