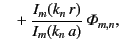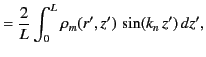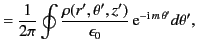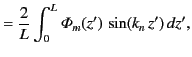Next: Exercises
Up: Potential Theory
Previous: Laplace's Equation in Cylindrical
Let us, finally, consider the solution of Poisson's equation,
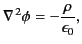 |
(442) |
in cylindrical coordinates. Suppose that the domain of solution extends over all space, and the potential
is subject to the simple boundary condition
In this case, the solution is written (see Section 2.3)
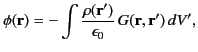 |
(444) |
where the integral is over all space, and
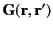 is a symmetric Green's function [i.e.,
is a symmetric Green's function [i.e.,
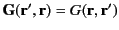 --see
Equation (143)] that satisfies
--see
Equation (143)] that satisfies
 |
(445) |
subject to the constraint [see Equation (143)]
In cylindrical coordinates,
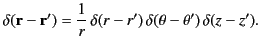 |
(447) |
This follows because, by definition (see Section 1.5),
 |
(448) |
whenever 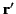 lies within the volume
lies within the volume  . Thus, Equation (446) becomes
. Thus, Equation (446) becomes
 |
(449) |
The well-known mathematical identities
are conventionally used to invert Fourier series and Fourier transforms, respectively.
In the present case, if we write
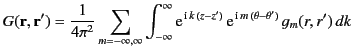 |
(452) |
then, making use of these identities, Equation (450) becomes
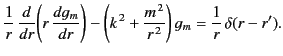 |
(453) |
In the general case, when 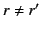 , the previous equation reduces to the modified Bessel equation,
, the previous equation reduces to the modified Bessel equation,
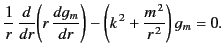 |
(454) |
As we saw in Section 3.10, the modified Bessel function 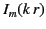 [defined in Equation (435)] is a solution of the modified Bessel
equation that is well behaved at
[defined in Equation (435)] is a solution of the modified Bessel
equation that is well behaved at
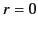 , and badly behaved as
, and badly behaved as
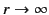 . On the other hand, the modified Bessel function
. On the other hand, the modified Bessel function 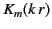 , where
, where![[*]](footnote.png)
 |
(455) |
is a solution that is badly behaved at 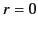 , and well behaved as
, and well behaved as
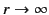 .
In fact,
.
In fact,
We are searching for a solution of Equation (454) that is well behaved at 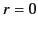 (because there is no reason
for the potential to be infinite at
(because there is no reason
for the potential to be infinite at 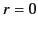 ) and goes to zero as
) and goes to zero as
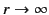 , in accordance with the constraint (447). It follows that
, in accordance with the constraint (447). It follows that
![$\displaystyle g_m(r,r')=\left\{\begin{array}{ccc}\alpha(r')\,I_m(k\,r)&\mbox{\hspace{1cm}}& r<r'\\ [0.5ex] \beta(r')\,K_m(k\,r)&&r>r'\end{array}\right..$](img969.png) |
(458) |
However, given that
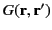 is a symmetric function, we expect
is a symmetric function, we expect  to also be symmetric: that is,
to also be symmetric: that is,
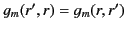 .
Consequently,
.
Consequently,
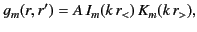 |
(459) |
where 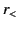 is the lesser of
is the lesser of 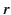 and
and  , and
, and 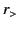 the greater. Integration of Equation (454) across
the greater. Integration of Equation (454) across 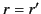 yields
yields
![$\displaystyle \left[\frac{d g_m}{dr}\right]_{r=r'_-}^{r=r'_+} = \frac{1}{r'},$](img975.png) |
(460) |
which implies that
![$\displaystyle A\,k\left[K_m'(k\,r')\,I_m(k\,r')-K_m(k\,r')\,I_m'(k\,r')\right] = \frac{1}{r'},$](img976.png) |
(461) |
where
 denotes differentiation with respect to argument. However, the modified Bessel functions
denotes differentiation with respect to argument. However, the modified Bessel functions 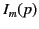 and
and  satisfy the well-known mathematical identity
satisfy the well-known mathematical identity![[*]](footnote.png)
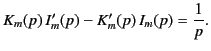 |
(462) |
Hence, we deduce that 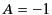 . Thus, our general Green's function becomes
. Thus, our general Green's function becomes
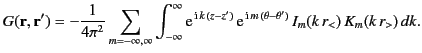 |
(463) |
The previous expression for the Green's function, in combination with Equation (445), leads to the following expressions for
the general solution to Poisson's equation in cylindrical geometry, subject to the boundary condition (444):
 |
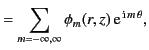 |
(464) |
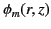 |
 |
(465) |
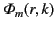 |
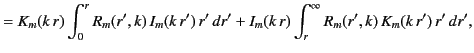 |
(466) |
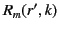 |
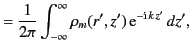 |
(467) |
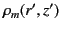 |
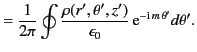 |
(468) |
Suppose that we wish to solve Poisson's equation within a finite cylindrical volume,  , bounded by the surfaces
, bounded by the surfaces 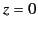 ,
, 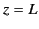 , and
, and
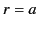 . Let the boundary conditions imposed at the surface be
. Let the boundary conditions imposed at the surface be
where
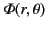 is a specified function. According to Section 2.10, the solution to this Dirichlet problem
is written
is a specified function. According to Section 2.10, the solution to this Dirichlet problem
is written
 |
(472) |
where  represents the bounding surface. Here, the Green's function is the symmetric solution to
represents the bounding surface. Here, the Green's function is the symmetric solution to
 |
(473) |
that satisfies
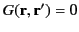 |
(474) |
when  (or
(or 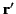 ) lies on
) lies on  .
.
As before, in cylindrical coordinates, Equation (474) is written
 |
(475) |
If we search for a separable solution of the form
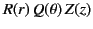 then it is clear that
then it is clear that
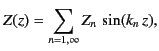 |
(476) |
where
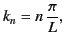 |
(477) |
is the appropriate expression for  that satisfies the constraint
that satisfies the constraint 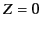 when
when 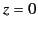 and
and 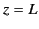 . The Fourier series
(477) can be inverted in the usual fashion to give
. The Fourier series
(477) can be inverted in the usual fashion to give
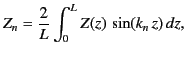 |
(478) |
which implies that
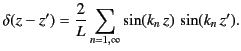 |
(479) |
Thus, searching for a Green's function of the form
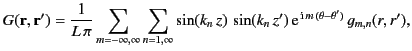 |
(480) |
Equation (476) reduces to
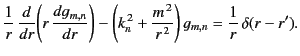 |
(481) |
Of course,
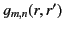 must be well behaved at
must be well behaved at 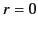 . Moreover, the constraint
. Moreover, the constraint
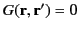 when
when 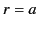 implies that
implies that
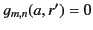 .
Hence,
.
Hence,
![$\displaystyle g_{m,n}(r,r')=\left\{\begin{array}{ccc}\alpha(r')\,I_m(k_n\,r)&\m...
...m(k_n\,r)\,K_m(k_n\,a)-I_m(k_n\,a)\,K_m(k_n\,r)\right]&&r>r'\end{array}\right..$](img1008.png) |
(482) |
Now, the Green's function must be continuous when 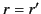 (otherwise, it would not be a symmetric function of
(otherwise, it would not be a symmetric function of  and
and 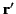 ): that is,
): that is,
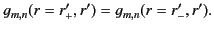 |
(483) |
This implies that
![$\displaystyle \alpha(r')\,I_m(k_n\,r') = \beta(r')\left[I_m(k_n\,r')\,K_m(k_n\,a)-I_m(k_n\,a)\,K_m(k_n\,r')\right].$](img1010.png) |
(484) |
Integration of Equation (476) across 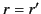 again gives (461), which leads to
again gives (461), which leads to
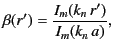 |
(485) |
where use has been made of Equations (463) and (485). It follows that
![$\displaystyle g_{m,n}(r,r') = -\left[I_m(k_n\,a)\,K_m(k_n\,r_>)- I_m(k_n\,r_>)\,K_m(k_n\,a)\right]\,\frac{I_m(k_n\,r_<)}{I_m(k_n\,a)}.$](img1012.png) |
(486) |
Our general expression for the Dirichlet Green's function becomes
It is easily demonstrated that
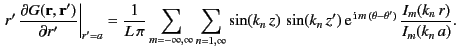 |
(488) |
Hence, making use of Equation (473), in combination with the previous two expressions, our general solution to the problem
under discussion is specified by the following set of equations:
 |
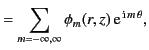 |
(489) |
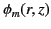 |
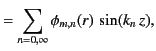 |
(490) |
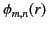 |
![$\displaystyle = \left[K_m(k_n\,r)-\frac{I_m(k_n\,r)\,K_m(k_n\,a)}{I_m(k_n\,a)}\right]\int_0^r R_{m,n}(r')\,I_m(k_n\,r')\,r'\,dr'$](img1019.png) |
|
| |
![$\displaystyle \phantom{=}+I_m(k_n\,r)\int_r^\infty R_{m,n}(r')\,\left[K_m(k_n\,r')-\frac{I_m(k_n\,r')\,K_m(k_n\,a)}{I_m(k_n\,a)}\right]r'\,dr'$](img1020.png) |
|
| |
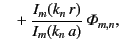 |
(491) |
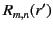 |
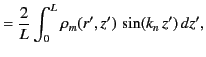 |
(492) |
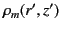 |
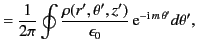 |
(493) |
 |
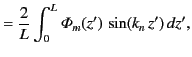 |
(494) |
 |
 |
(495) |



Next: Exercises
Up: Potential Theory
Previous: Laplace's Equation in Cylindrical
Richard Fitzpatrick
2014-06-27
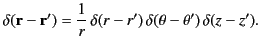

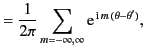
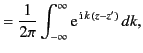
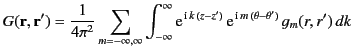
![]() , the previous equation reduces to the modified Bessel equation,
, the previous equation reduces to the modified Bessel equation,
![[*]](footnote.png)

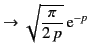
![]() (because there is no reason
for the potential to be infinite at
(because there is no reason
for the potential to be infinite at ![]() ) and goes to zero as
) and goes to zero as
![]() , in accordance with the constraint (447). It follows that
, in accordance with the constraint (447). It follows that
![$\displaystyle g_m(r,r')=\left\{\begin{array}{ccc}\alpha(r')\,I_m(k\,r)&\mbox{\hspace{1cm}}& r<r'\\ [0.5ex] \beta(r')\,K_m(k\,r)&&r>r'\end{array}\right..$](img969.png)
![$\displaystyle A\,k\left[K_m'(k\,r')\,I_m(k\,r')-K_m(k\,r')\,I_m'(k\,r')\right] = \frac{1}{r'},$](img976.png)
![[*]](footnote.png)
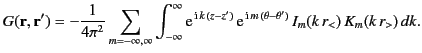
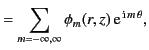

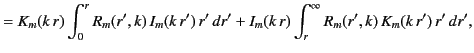
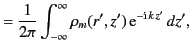
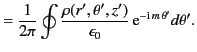
![]() , bounded by the surfaces
, bounded by the surfaces ![]() ,
, ![]() , and
, and
![]() . Let the boundary conditions imposed at the surface be
. Let the boundary conditions imposed at the surface be
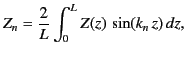
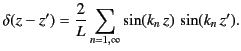
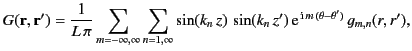
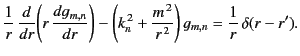
![$\displaystyle g_{m,n}(r,r')=\left\{\begin{array}{ccc}\alpha(r')\,I_m(k_n\,r)&\m...
...m(k_n\,r)\,K_m(k_n\,a)-I_m(k_n\,a)\,K_m(k_n\,r)\right]&&r>r'\end{array}\right..$](img1008.png)
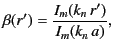
![$\displaystyle g_{m,n}(r,r') = -\left[I_m(k_n\,a)\,K_m(k_n\,r_>)- I_m(k_n\,r_>)\,K_m(k_n\,a)\right]\,\frac{I_m(k_n\,r_<)}{I_m(k_n\,a)}.$](img1012.png)

![$\displaystyle \phantom{==}\left[I_m(k_n\,a)\,K_m(k_n\,r_>)- I_m(k_n\,r_>)\,K_m(k_n\,a)\right]\,\frac{I_m(k_n\,r_<)}{I_m(k_n\,a)}.$](img1015.png)
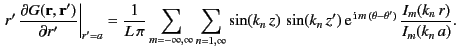
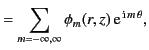
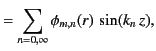
![$\displaystyle = \left[K_m(k_n\,r)-\frac{I_m(k_n\,r)\,K_m(k_n\,a)}{I_m(k_n\,a)}\right]\int_0^r R_{m,n}(r')\,I_m(k_n\,r')\,r'\,dr'$](img1019.png)
![$\displaystyle \phantom{=}+I_m(k_n\,r)\int_r^\infty R_{m,n}(r')\,\left[K_m(k_n\,r')-\frac{I_m(k_n\,r')\,K_m(k_n\,a)}{I_m(k_n\,a)}\right]r'\,dr'$](img1020.png)