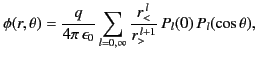Next: Dirichlet Problem in Spherical
Up: Potential Theory
Previous: Multipole Expansion
Axisymmetric Charge Distributions
For the case of an axisymmetric charge distribution (i.e., a charge distribution that is independent of the azimuthal angle 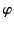 ), we
can neglect the spherical harmonics of non-zero order (i.e., the non-axisymmetric harmonics) in Equation (335), which reduces to the
following expression for the general axisymmetric Green's function:
), we
can neglect the spherical harmonics of non-zero order (i.e., the non-axisymmetric harmonics) in Equation (335), which reduces to the
following expression for the general axisymmetric Green's function:
 |
(364) |
Here, use have been made of the fact that [see Equation (309)]
 |
(365) |
In this case, the general solution to Poisson's equation, (337), reduces to
![$\displaystyle \phi({\bf r}) = \frac{1}{4\pi\,\epsilon_0}\sum_{l=0,\infty}\left[r^{\,l}\,p_{l}(r)+ \frac{q_{l}(r)}{r^{\,l+1}}\right]P_l(\cos\theta),$](img817.png) |
(366) |
where
Consider the potential generated by a charge 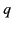 distributed uniformly in a thin ring of radius
distributed uniformly in a thin ring of radius 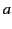 that lies in the
that lies in the 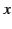 -
-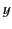 plane, and
is centered at the origin. It follows that
plane, and
is centered at the origin. It follows that
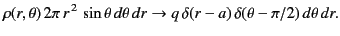 |
(369) |
Hence, for 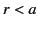 we obtain
we obtain 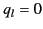 and
and
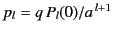 . On the other hand, for
. On the other hand, for 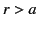 we get
we get
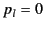 and
and
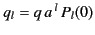 . Thus,
. Thus,
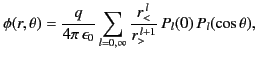 |
(370) |
where 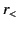 represents the lesser of
represents the lesser of 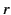 and
and 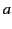 , whereas
, whereas 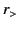 represents the greater.
represents the greater.



Next: Dirichlet Problem in Spherical
Up: Potential Theory
Previous: Multipole Expansion
Richard Fitzpatrick
2014-06-27
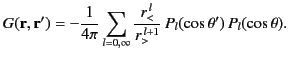
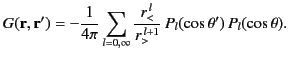
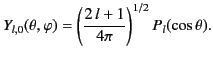
![$\displaystyle \phi({\bf r}) = \frac{1}{4\pi\,\epsilon_0}\sum_{l=0,\infty}\left[r^{\,l}\,p_{l}(r)+ \frac{q_{l}(r)}{r^{\,l+1}}\right]P_l(\cos\theta),$](img817.png)
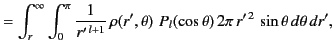
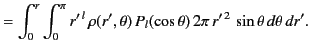
![]() distributed uniformly in a thin ring of radius
distributed uniformly in a thin ring of radius ![]() that lies in the
that lies in the ![]() -
-![]() plane, and
is centered at the origin. It follows that
plane, and
is centered at the origin. It follows that