


Next: WKB Solution as Asymptotic
Up: Wave Propagation in Inhomogeneous
Previous: Ionospheric Ray Tracing
Asymptotic Series
It is often convenient to expand a function of the complex variable
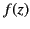 as a series in inverse powers of
as a series in inverse powers of  . For example,
. For example,
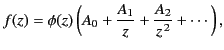 |
(1148) |
where  is a function whose behavior for large values
of
is a function whose behavior for large values
of  is known. If
is known. If
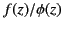 is singular as
is singular as
 then the previous series clearly diverges. Nevertheless,
under certain circumstances, the series may still
be useful.
In fact, this is the case if the difference
between
then the previous series clearly diverges. Nevertheless,
under certain circumstances, the series may still
be useful.
In fact, this is the case if the difference
between
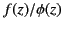 and the first
and the first 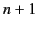 terms is of
order
terms is of
order
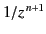 , so that for sufficiently large
, so that for sufficiently large  this difference
becomes vanishingly small. More precisely, the series is said to
represent
this difference
becomes vanishingly small. More precisely, the series is said to
represent
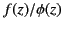 asymptotically, that is
asymptotically, that is
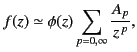 |
(1149) |
provided that
![$\displaystyle \lim_{\vert z\vert\rightarrow\infty} \left( z^{\,n} \left[ \frac{f(z)}{\phi(z)} - \sum_{p=0,n}\frac{A_p}{z^{\,p}}\right]\right) \rightarrow 0.$](img2408.png) |
(1150) |
In other words, for a given value of  , the sum of the first
, the sum of the first 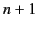 terms of the
series may be made as close as desired to the ratio
terms of the
series may be made as close as desired to the ratio
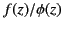 by making
by making  sufficiently large. For each value of
sufficiently large. For each value of  and
and  there is an
error in the series representation of
there is an
error in the series representation of
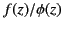 which is of order
which is of order
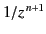 . Because the series actually diverges, there is
an optimum number of terms in the series used to represent
. Because the series actually diverges, there is
an optimum number of terms in the series used to represent
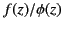 for a given value of
for a given value of  . Associated with this is
an unavoidable error. As
. Associated with this is
an unavoidable error. As  increases, the optimal number of
terms increases, and the error decreases.
increases, the optimal number of
terms increases, and the error decreases.
Consider a simple example. The exponential integral is defined
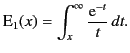 |
(1151) |
The asymptotic series for this function can be generated via
a series of partial integrations. For example,
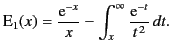 |
(1152) |
A continuation of this procedure yields
![$\displaystyle {\rm E}_1(x) = \frac{{\rm e}^{-x}}{x}\left[ 1-\frac{1}{x} + \frac...
...\,n}}\right] +(-1)^{n+1}(n+1)!\int_x^\infty \frac{{\rm e}^{-t}}{t^{\,n+2}}\,dt.$](img2411.png) |
(1153) |
The infinite series obtained by taking the limit
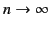 diverges, because the Cauchy convergence test yields
diverges, because the Cauchy convergence test yields
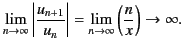 |
(1154) |
Note that two successive terms in the series become equal in magnitude
for  , indicating that the optimum number of terms for a given
, indicating that the optimum number of terms for a given  is roughly the nearest integer to
is roughly the nearest integer to  . To prove that the series is
asymptotic, we need to show that
. To prove that the series is
asymptotic, we need to show that
 |
(1155) |
This immediately follows, because
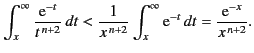 |
(1156) |
Thus, the error involved in using the first  terms in the series is less than
terms in the series is less than
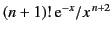 , which is the magnitude of the next term in the
series. We can see that, as
, which is the magnitude of the next term in the
series. We can see that, as  increases, this estimate of the
error first decreases, and then increases without limit.
In order to visualize this phenomenon more exactly,
let
increases, this estimate of the
error first decreases, and then increases without limit.
In order to visualize this phenomenon more exactly,
let
 , and let
, and let
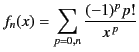 |
(1157) |
be the asymptotic series representation of this function that
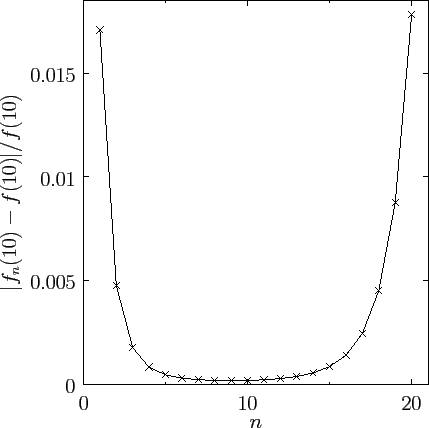
contains 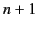 terms. Figure 21 shows the
relative error in the
asymptotic series
terms. Figure 21 shows the
relative error in the
asymptotic series
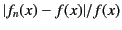 plotted as a function of
the approximate number of terms in the series,
plotted as a function of
the approximate number of terms in the series,  , for
, for  . It can be seen that as
. It can be seen that as  increases the
error initially falls, reaches
a minimum value at about
increases the
error initially falls, reaches
a minimum value at about 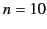 , and then increases rapidly. Clearly,
the optimum number of terms in the asymptotic series used to
represent
, and then increases rapidly. Clearly,
the optimum number of terms in the asymptotic series used to
represent  is about 10.
is about 10.
Figure 21:
The relative error in a typical asymptotic series plotted
as a function of the number of terms in the series.
 |
Asymptotic series are fundamentally different to conventional power
law expansions, such as
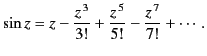 |
(1158) |
This series representation of 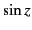 converges absolutely for all
finite values of
converges absolutely for all
finite values of  . Thus, at any
. Thus, at any  ,
the error associated with the series can
be made as small as is desired by including a sufficiently
large number of terms.
In other words, unlike an asymptotic series, there is no intrinsic,
or unavoidable, error associated with a convergent series.
It follows that a convergent
power law series representation of a function is unique within
the domain of convergence of the series. On the
other hand, an asymptotic series representation
of a function is not unique. It is
perfectly possible to have two different
asymptotic series representations of the same function, as long as
the difference between the two series is less than the intrinsic error
associated with each series. Furthermore, it is often the case that
different asymptotic series are used to represent the
same single-valued
analytic
function
in different regions of the complex plane.
,
the error associated with the series can
be made as small as is desired by including a sufficiently
large number of terms.
In other words, unlike an asymptotic series, there is no intrinsic,
or unavoidable, error associated with a convergent series.
It follows that a convergent
power law series representation of a function is unique within
the domain of convergence of the series. On the
other hand, an asymptotic series representation
of a function is not unique. It is
perfectly possible to have two different
asymptotic series representations of the same function, as long as
the difference between the two series is less than the intrinsic error
associated with each series. Furthermore, it is often the case that
different asymptotic series are used to represent the
same single-valued
analytic
function
in different regions of the complex plane.
For example, consider
the asymptotic expansion of the confluent hypergeometric function
 . This
function is the solution of the differential equation
. This
function is the solution of the differential equation
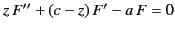 |
(1159) |
which is analytic at 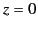 [in fact,
[in fact,
 ]. Here,
]. Here,  denotes
denotes
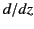 . The asymptotic expansion of
. The asymptotic expansion of  takes the form:
takes the form:
for
 , and
, and
for
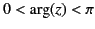 , and
, and
for
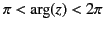 , et cetera.
Here,
, et cetera.
Here,
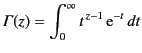 |
(1163) |
is a so-called Gamma function. This function has the property that
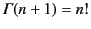 , where
, where  is
a non-negative integer.
It can be seen that the expansion consists of
a linear combination of two asymptotic series (only the
first term in each series is shown). For
is
a non-negative integer.
It can be seen that the expansion consists of
a linear combination of two asymptotic series (only the
first term in each series is shown). For 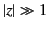 , the first series
is exponentially larger than the second whenever
, the first series
is exponentially larger than the second whenever
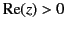 .
The first series is said to be dominant in this region, whereas
the second series is said to be subdominant. Likewise, the first
series is exponentially smaller than the second whenever
.
The first series is said to be dominant in this region, whereas
the second series is said to be subdominant. Likewise, the first
series is exponentially smaller than the second whenever
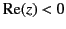 . Hence, the first series is subdominant, and the
second series dominant, in this region.
. Hence, the first series is subdominant, and the
second series dominant, in this region.
Consider a region in which
one or other of the series is dominant. Strictly speaking, it is
not mathematically consistent to include the subdominant series in
the asymptotic expansion, because its contribution is actually
less than the intrinsic error associated with the dominant series
[this error is
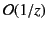 times the dominant series, because we are only
including the first term in this series]. Thus, at a general point
in the complex plane, the asymptotic expansion simply consists
of the dominant series. However, this is not the case
in the immediate vicinity of the lines
times the dominant series, because we are only
including the first term in this series]. Thus, at a general point
in the complex plane, the asymptotic expansion simply consists
of the dominant series. However, this is not the case
in the immediate vicinity of the lines
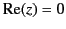 , which are
called anti-Stokes lines. When an anti-Stokes line is
crossed, a dominant series becomes subdominant, and vice versa.
Thus, in the immediate vicinity of an anti-Stokes line neither
series is dominant, so it is mathematically consistent to include
both series in the asymptotic expansion.
, which are
called anti-Stokes lines. When an anti-Stokes line is
crossed, a dominant series becomes subdominant, and vice versa.
Thus, in the immediate vicinity of an anti-Stokes line neither
series is dominant, so it is mathematically consistent to include
both series in the asymptotic expansion.
The hypergeometric function  is a perfectly well-behaved,
single-valued, analytic function in the complex plane. However, our
two asymptotic series are, in general, multi-valued functions in the
complex plane [see Equation (1162)]. Can a single-valued function
be represented asymptotically by a multi-valued function? The short answer
is no. We have to employ different combinations of
the two series in different
regions of the complex plane in order to ensure that
is a perfectly well-behaved,
single-valued, analytic function in the complex plane. However, our
two asymptotic series are, in general, multi-valued functions in the
complex plane [see Equation (1162)]. Can a single-valued function
be represented asymptotically by a multi-valued function? The short answer
is no. We have to employ different combinations of
the two series in different
regions of the complex plane in order to ensure that  remains
single-valued. Equations (1162)-(1164) show how this is achieved.
Basically, the coefficient in front of the subdominant series
changes discontinuously at certain values of
remains
single-valued. Equations (1162)-(1164) show how this is achieved.
Basically, the coefficient in front of the subdominant series
changes discontinuously at certain values of
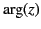 . This
is perfectly consistent with
. This
is perfectly consistent with  being an analytic function
because the subdominant series is ``invisible'': in other words, the contribution
of the subdominant series to the asymptotic solution falls below the
intrinsic error associated with the dominant series, so that it does not really
matter if the coefficient in front of the former series
changes discontinuously. Imagine tracing a large circle, centered on the
origin, in the complex plane. Close to an anti-Stokes line, neither
series is dominant, so we must include both series in the asymptotic
expansion. As we move away from the anti-Stokes line, one series
becomes dominant, which means that the other series becomes
subdominant, and, therefore, drops out of our asymptotic expansion.
Eventually, we approach a second anti-Stokes line, and the subdominant
series reappears in our asymptotic expansion. However, the
coefficient in front of the subdominant series, when it
reappears, is different to that when the series disappeared. This new
coefficient is carried across the second anti-Stokes line into the
region where the subdominant series becomes dominant. In this new
region, the dominant series becomes subdominant, and disappears
from our asymptotic expansion. Eventually, a third anti-Stokes line
is approached, and the series reappears, but, again, with a different
coefficient in front. The jumps in the coefficients of the subdominant series
are chosen in such a manner that if we perform a complete circuit in the complex
plane then the value of the asymptotic expansion is the same at the beginning
and the
end points. In other words, the asymptotic expansion is single-valued,
despite the fact that it is built up out of two asymptotic
series that are not single-valued. The jumps in the coefficient of the
subdominant series, which are needed to keep the asymptotic expansion
single-valued, are called Stokes phenomena, after the
celebrated nineteenth century British mathematician
Sir George Gabriel Stokes, who first drew attention to this effect.
being an analytic function
because the subdominant series is ``invisible'': in other words, the contribution
of the subdominant series to the asymptotic solution falls below the
intrinsic error associated with the dominant series, so that it does not really
matter if the coefficient in front of the former series
changes discontinuously. Imagine tracing a large circle, centered on the
origin, in the complex plane. Close to an anti-Stokes line, neither
series is dominant, so we must include both series in the asymptotic
expansion. As we move away from the anti-Stokes line, one series
becomes dominant, which means that the other series becomes
subdominant, and, therefore, drops out of our asymptotic expansion.
Eventually, we approach a second anti-Stokes line, and the subdominant
series reappears in our asymptotic expansion. However, the
coefficient in front of the subdominant series, when it
reappears, is different to that when the series disappeared. This new
coefficient is carried across the second anti-Stokes line into the
region where the subdominant series becomes dominant. In this new
region, the dominant series becomes subdominant, and disappears
from our asymptotic expansion. Eventually, a third anti-Stokes line
is approached, and the series reappears, but, again, with a different
coefficient in front. The jumps in the coefficients of the subdominant series
are chosen in such a manner that if we perform a complete circuit in the complex
plane then the value of the asymptotic expansion is the same at the beginning
and the
end points. In other words, the asymptotic expansion is single-valued,
despite the fact that it is built up out of two asymptotic
series that are not single-valued. The jumps in the coefficient of the
subdominant series, which are needed to keep the asymptotic expansion
single-valued, are called Stokes phenomena, after the
celebrated nineteenth century British mathematician
Sir George Gabriel Stokes, who first drew attention to this effect.
Where exactly does the jump in the coefficient of the subdominant
series occur? All we can really say is ``somewhere in the
region between two anti-Stokes lines where the series in question
is subdominant.'' The problem is that we only retained the
first term in each asymptotic series. Consequently, the intrinsic
error in
the dominant series is relatively large, and we lose track of
the subdominant series very quickly after moving away from
an anti-Stokes line. However, we could include more terms in each
asymptotic series. This would enable us to reduce the intrinsic error in
the dominant series, and, thereby, expand the region of the complex
plane in the vicinity of the anti-Stokes lines where
we can see both the dominant
and subdominant series. If we were to keep adding terms to our
asymptotic series, so as to minimize the error in the dominant
solution, we would eventually be forced to conclude that a jump in the
coefficient of the subdominant series can only take place on
those lines
in the complex plane on which
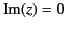 : these are
called Stokes lines. This result was first proved by Stokes in 1857.
: these are
called Stokes lines. This result was first proved by Stokes in 1857.![[*]](footnote.png) On a Stokes line, the magnitude of the dominant
series achieves its maximum value with respect to that of
the subdominant series. Once we know that a jump in the coefficient
of the subdominant series can only take place at a Stokes line,
we can retain the subdominant series in our asymptotic expansion
in all regions of the complex plane. What we are basically saying is that,
although, in practice,
we cannot actually see the subdominant series very far away
from an anti-Stokes line, because we are only retaining the
first term in each asymptotic series, we could, in principle, see the
subdominant series at all values of
On a Stokes line, the magnitude of the dominant
series achieves its maximum value with respect to that of
the subdominant series. Once we know that a jump in the coefficient
of the subdominant series can only take place at a Stokes line,
we can retain the subdominant series in our asymptotic expansion
in all regions of the complex plane. What we are basically saying is that,
although, in practice,
we cannot actually see the subdominant series very far away
from an anti-Stokes line, because we are only retaining the
first term in each asymptotic series, we could, in principle, see the
subdominant series at all values of
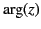 provided that
we retained a sufficient number of terms in our asymptotic series.
provided that
we retained a sufficient number of terms in our asymptotic series.
Figure 22:
The
location of the Stokes lines (dashed), the anti-Stokes lines
(solid), and the branch cut (wavy) in the complex plane
for the asymptotic expansion of the hypergeometric function.
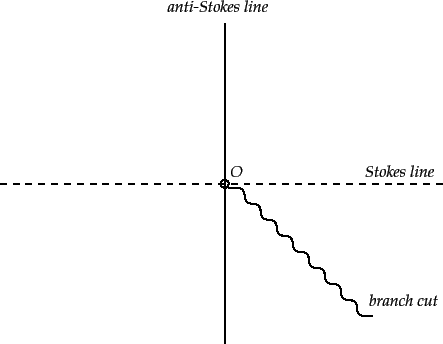 |
Figure 784 shows the location in the complex plane
of the Stokes and anti-Stokes lines
for the asymptotic expansion of the hypergeometric function. Also
shown is a branch cut, which is needed to make  single-valued. The
branch cut is chosen such that
single-valued. The
branch cut is chosen such that
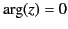 on the positive
real axis.
Every time we cross an anti-Stokes line, the dominant series becomes
subdominant, and vice versa. Every time we cross a Stokes line,
the coefficient in front of the dominant series stays the same, but that in
front of the subdominant series jumps discontinuously [see Equations (1162)-(1164)].
Finally, the jumps in the coefficient of the subdominant series are such
as to ensure that the asymptotic expansion is single-valued.
on the positive
real axis.
Every time we cross an anti-Stokes line, the dominant series becomes
subdominant, and vice versa. Every time we cross a Stokes line,
the coefficient in front of the dominant series stays the same, but that in
front of the subdominant series jumps discontinuously [see Equations (1162)-(1164)].
Finally, the jumps in the coefficient of the subdominant series are such
as to ensure that the asymptotic expansion is single-valued.



Next: WKB Solution as Asymptotic
Up: Wave Propagation in Inhomogeneous
Previous: Ionospheric Ray Tracing
Richard Fitzpatrick
2014-06-27
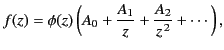
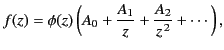
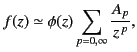
![$\displaystyle \lim_{\vert z\vert\rightarrow\infty} \left( z^{\,n} \left[ \frac{f(z)}{\phi(z)} - \sum_{p=0,n}\frac{A_p}{z^{\,p}}\right]\right) \rightarrow 0.$](img2408.png)
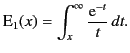
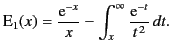
![$\displaystyle {\rm E}_1(x) = \frac{{\rm e}^{-x}}{x}\left[ 1-\frac{1}{x} + \frac...
...\,n}}\right] +(-1)^{n+1}(n+1)!\int_x^\infty \frac{{\rm e}^{-t}}{t^{\,n+2}}\,dt.$](img2411.png)
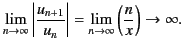

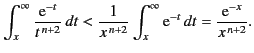
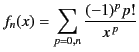

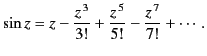
![]() . This
function is the solution of the differential equation
. This
function is the solution of the differential equation
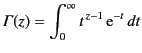
![]() times the dominant series, because we are only
including the first term in this series]. Thus, at a general point
in the complex plane, the asymptotic expansion simply consists
of the dominant series. However, this is not the case
in the immediate vicinity of the lines
times the dominant series, because we are only
including the first term in this series]. Thus, at a general point
in the complex plane, the asymptotic expansion simply consists
of the dominant series. However, this is not the case
in the immediate vicinity of the lines
![]() , which are
called anti-Stokes lines. When an anti-Stokes line is
crossed, a dominant series becomes subdominant, and vice versa.
Thus, in the immediate vicinity of an anti-Stokes line neither
series is dominant, so it is mathematically consistent to include
both series in the asymptotic expansion.
, which are
called anti-Stokes lines. When an anti-Stokes line is
crossed, a dominant series becomes subdominant, and vice versa.
Thus, in the immediate vicinity of an anti-Stokes line neither
series is dominant, so it is mathematically consistent to include
both series in the asymptotic expansion.
![]() is a perfectly well-behaved,
single-valued, analytic function in the complex plane. However, our
two asymptotic series are, in general, multi-valued functions in the
complex plane [see Equation (1162)]. Can a single-valued function
be represented asymptotically by a multi-valued function? The short answer
is no. We have to employ different combinations of
the two series in different
regions of the complex plane in order to ensure that
is a perfectly well-behaved,
single-valued, analytic function in the complex plane. However, our
two asymptotic series are, in general, multi-valued functions in the
complex plane [see Equation (1162)]. Can a single-valued function
be represented asymptotically by a multi-valued function? The short answer
is no. We have to employ different combinations of
the two series in different
regions of the complex plane in order to ensure that ![]() remains
single-valued. Equations (1162)-(1164) show how this is achieved.
Basically, the coefficient in front of the subdominant series
changes discontinuously at certain values of
remains
single-valued. Equations (1162)-(1164) show how this is achieved.
Basically, the coefficient in front of the subdominant series
changes discontinuously at certain values of
![]() . This
is perfectly consistent with
. This
is perfectly consistent with ![]() being an analytic function
because the subdominant series is ``invisible'': in other words, the contribution
of the subdominant series to the asymptotic solution falls below the
intrinsic error associated with the dominant series, so that it does not really
matter if the coefficient in front of the former series
changes discontinuously. Imagine tracing a large circle, centered on the
origin, in the complex plane. Close to an anti-Stokes line, neither
series is dominant, so we must include both series in the asymptotic
expansion. As we move away from the anti-Stokes line, one series
becomes dominant, which means that the other series becomes
subdominant, and, therefore, drops out of our asymptotic expansion.
Eventually, we approach a second anti-Stokes line, and the subdominant
series reappears in our asymptotic expansion. However, the
coefficient in front of the subdominant series, when it
reappears, is different to that when the series disappeared. This new
coefficient is carried across the second anti-Stokes line into the
region where the subdominant series becomes dominant. In this new
region, the dominant series becomes subdominant, and disappears
from our asymptotic expansion. Eventually, a third anti-Stokes line
is approached, and the series reappears, but, again, with a different
coefficient in front. The jumps in the coefficients of the subdominant series
are chosen in such a manner that if we perform a complete circuit in the complex
plane then the value of the asymptotic expansion is the same at the beginning
and the
end points. In other words, the asymptotic expansion is single-valued,
despite the fact that it is built up out of two asymptotic
series that are not single-valued. The jumps in the coefficient of the
subdominant series, which are needed to keep the asymptotic expansion
single-valued, are called Stokes phenomena, after the
celebrated nineteenth century British mathematician
Sir George Gabriel Stokes, who first drew attention to this effect.
being an analytic function
because the subdominant series is ``invisible'': in other words, the contribution
of the subdominant series to the asymptotic solution falls below the
intrinsic error associated with the dominant series, so that it does not really
matter if the coefficient in front of the former series
changes discontinuously. Imagine tracing a large circle, centered on the
origin, in the complex plane. Close to an anti-Stokes line, neither
series is dominant, so we must include both series in the asymptotic
expansion. As we move away from the anti-Stokes line, one series
becomes dominant, which means that the other series becomes
subdominant, and, therefore, drops out of our asymptotic expansion.
Eventually, we approach a second anti-Stokes line, and the subdominant
series reappears in our asymptotic expansion. However, the
coefficient in front of the subdominant series, when it
reappears, is different to that when the series disappeared. This new
coefficient is carried across the second anti-Stokes line into the
region where the subdominant series becomes dominant. In this new
region, the dominant series becomes subdominant, and disappears
from our asymptotic expansion. Eventually, a third anti-Stokes line
is approached, and the series reappears, but, again, with a different
coefficient in front. The jumps in the coefficients of the subdominant series
are chosen in such a manner that if we perform a complete circuit in the complex
plane then the value of the asymptotic expansion is the same at the beginning
and the
end points. In other words, the asymptotic expansion is single-valued,
despite the fact that it is built up out of two asymptotic
series that are not single-valued. The jumps in the coefficient of the
subdominant series, which are needed to keep the asymptotic expansion
single-valued, are called Stokes phenomena, after the
celebrated nineteenth century British mathematician
Sir George Gabriel Stokes, who first drew attention to this effect.
![]() : these are
called Stokes lines. This result was first proved by Stokes in 1857.
: these are
called Stokes lines. This result was first proved by Stokes in 1857.![[*]](footnote.png) On a Stokes line, the magnitude of the dominant
series achieves its maximum value with respect to that of
the subdominant series. Once we know that a jump in the coefficient
of the subdominant series can only take place at a Stokes line,
we can retain the subdominant series in our asymptotic expansion
in all regions of the complex plane. What we are basically saying is that,
although, in practice,
we cannot actually see the subdominant series very far away
from an anti-Stokes line, because we are only retaining the
first term in each asymptotic series, we could, in principle, see the
subdominant series at all values of
On a Stokes line, the magnitude of the dominant
series achieves its maximum value with respect to that of
the subdominant series. Once we know that a jump in the coefficient
of the subdominant series can only take place at a Stokes line,
we can retain the subdominant series in our asymptotic expansion
in all regions of the complex plane. What we are basically saying is that,
although, in practice,
we cannot actually see the subdominant series very far away
from an anti-Stokes line, because we are only retaining the
first term in each asymptotic series, we could, in principle, see the
subdominant series at all values of
![]() provided that
we retained a sufficient number of terms in our asymptotic series.
provided that
we retained a sufficient number of terms in our asymptotic series.

![]() single-valued. The
branch cut is chosen such that
single-valued. The
branch cut is chosen such that
![]() on the positive
real axis.
Every time we cross an anti-Stokes line, the dominant series becomes
subdominant, and vice versa. Every time we cross a Stokes line,
the coefficient in front of the dominant series stays the same, but that in
front of the subdominant series jumps discontinuously [see Equations (1162)-(1164)].
Finally, the jumps in the coefficient of the subdominant series are such
as to ensure that the asymptotic expansion is single-valued.
on the positive
real axis.
Every time we cross an anti-Stokes line, the dominant series becomes
subdominant, and vice versa. Every time we cross a Stokes line,
the coefficient in front of the dominant series stays the same, but that in
front of the subdominant series jumps discontinuously [see Equations (1162)-(1164)].
Finally, the jumps in the coefficient of the subdominant series are such
as to ensure that the asymptotic expansion is single-valued.