


Next: Electromagnetic Energy Conservation
Up: Maxwell's Equations
Previous: Retarded Potentials
Retarded Fields
We have found the solution to Maxwell's equations in terms of retarded potentials. Let us now
construct the associated retarded electric and magnetic fields using (see Section 1.3)
It is helpful to write
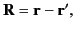 |
(79) |
where
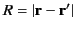 . The retarded time becomes
. The retarded time becomes
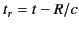 , and a general retarded
quantity is written
, and a general retarded
quantity is written
![$ [F({\bf r}', t)]\equiv F({\bf r}', t_r)$](img222.png) . Thus, we can express the retarded
potential solutions of Maxwell's equations in the particularly compact form
. Thus, we can express the retarded
potential solutions of Maxwell's equations in the particularly compact form
It is easily seen that
where use has been made of
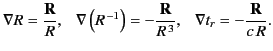 |
(83) |
Likewise,
Equations (77), (78), (82), and (84) can be combined to give
![$\displaystyle {\bf E} = \frac{1}{4\pi\,\epsilon_0} \int \left( [\rho] \,\frac{\...
... R}{c\,R^{\,2}} - \frac{[\partial {\bf j}/\partial t]}{c^{\,2} \,R} \right)dV',$](img232.png) |
(85) |
and
![$\displaystyle {\bf B} = \frac{\mu_0}{4\pi} \int \left( \frac{ [{\bf j}]\times {...
...+ \frac{ [\partial {\bf j}/\partial t]\times {\bf R} } {c\,R^{\,2}} \right)dV'.$](img233.png) |
(86) |
Suppose that our charges and currents vary on some characteristic timescale 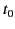 . Let
us define
. Let
us define
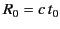 , which is the distance a light ray travels in time
, which is the distance a light ray travels in time 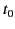 . We
can evaluate Equations (85) and (86) in two asymptotic regions: the near field
region
. We
can evaluate Equations (85) and (86) in two asymptotic regions: the near field
region 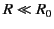 , and the far field region
, and the far field region 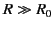 . In the near field region,
. In the near field region,
 |
(87) |
so the difference between retarded time and standard time is relatively small. This
allows us to expand retarded quantities in a Taylor series. Thus,
![$\displaystyle [\rho] \simeq \rho + \frac{\partial\rho}{\partial t} \,(t_r-t) + \frac{1}{2} \frac{\partial^{\,2} \rho}{\partial t^{\,2}}\,(t_r -t )^2+\cdots,$](img239.png) |
(88) |
giving
![$\displaystyle [\rho] \simeq \rho - \frac{\partial \rho}{\partial t} \frac{R}{c}...
... \frac{\partial^{\,2} \rho}{\partial t^{\,2}} \frac{R^{\,2}}{c^{\,2}} + \cdots.$](img240.png) |
(89) |
Expansion of the retarded quantities in the near field region yields
In Equation (90), the first term on the right-hand side corresponds to Coulomb's law, the second
term is the lowest order correction to Coulomb's law due to retardation effects, and the third term corresponds to Faraday
induction. In Equation (91), the first term on the right-hand side is the Biot-Savart law,
and the second term is the lowest order correction to the Biot-Savart law due to retardation effects. Note that the retardation
corrections are only of order 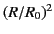 . We might suppose, from looking at Equations (85) and
(86), that the corrections should be of order
. We might suppose, from looking at Equations (85) and
(86), that the corrections should be of order 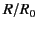 . However, all of the order
. However, all of the order 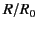 terms canceled out in the previous expansion.
terms canceled out in the previous expansion.
In the far field region, 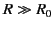 , Equations (85) and (86) are dominated by the terms that
vary like
, Equations (85) and (86) are dominated by the terms that
vary like  , so that
, so that
where
 |
(94) |
Here, use has been made of
![$ [\partial \rho/\partial t] = -[\nabla\cdot {\bf j}]$](img251.png) and
and
![$ [\nabla\cdot {\bf j} ] \simeq -[\partial {\bf j}/\partial t]\cdot {\bf R}/(c \,R)$](img252.png) .
Suppose that our charges and currents are localized to some finite region of space in the vicinity of the origin, and that the extent of the
current-and-charge-containing region is much less than
.
Suppose that our charges and currents are localized to some finite region of space in the vicinity of the origin, and that the extent of the
current-and-charge-containing region is much less than 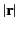 .
It follows that retarded quantities can be written
.
It follows that retarded quantities can be written
![$\displaystyle [ \rho({\bf r}', t)] \simeq \rho({\bf r}', t - r/c),$](img254.png) |
(95) |
et cetera. Thus, the electric field reduces to
![$\displaystyle {\bf E}({\bf r},t) \simeq -\frac{1}{4\pi\,\epsilon_0} \frac{\left[ \int \partial {\bf j}_\perp/\partial t\,\,dV'\right]}{c^{\,2}\, r},$](img255.png) |
(96) |
whereas the magnetic field is given by
![$\displaystyle {\bf B}({\bf r},t) \simeq \frac{1}{4\pi\,\epsilon_0} \frac{ \left...
...ial {\bf j}_\perp /\partial t\,\,dV'\right] \times{\bf r} }{c^{\,3} \,r^{\,2}}.$](img256.png) |
(97) |
Here, ![$ [\cdots]$](img257.png) merely denotes evaluation at the retarded time
merely denotes evaluation at the retarded time 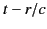 .
Note that
.
Note that
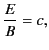 |
(98) |
and
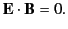 |
(99) |
This configuration of electric and magnetic fields is characteristic of an electromagnetic wave.
In fact, Equations (96) and (97) describe an electromagnetic wave propagating radially
away from the
charge and current containing region. The wave is clearly driven by time-varying electric
currents. Now, charges moving with a constant velocity constitute a steady current, so a
nonsteady current is associated with accelerating charges. We conclude that accelerating
electric charges emit electromagnetic waves. The wave fields, (96) and (97), fall off
like the inverse of the distance from the wave source. This behavior should be contrasted with
that of Coulomb or Biot-Savart fields, which fall off like the inverse square of
the distance from the source.
In conclusion, electric and magnetic fields look simple in the near field region (they are
just Coulomb fields, etc.), and also in the far field region (they are just electromagnetic
waves). Only in the intermediate region, 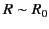 , do the fields get really complicated.
, do the fields get really complicated.



Next: Electromagnetic Energy Conservation
Up: Maxwell's Equations
Previous: Retarded Potentials
Richard Fitzpatrick
2014-06-27
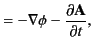
![$\displaystyle = \frac{1}{4\pi\, \epsilon_0} \int \frac{[\rho]}{R} \,dV',$](img223.png)
![$\displaystyle = \frac{\mu_0}{4\pi} \int \frac{[{\bf j}]}{R} \,dV'.$](img224.png)
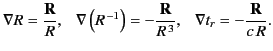
![]() . Let
us define
. Let
us define
![]() , which is the distance a light ray travels in time
, which is the distance a light ray travels in time ![]() . We
can evaluate Equations (85) and (86) in two asymptotic regions: the near field
region
. We
can evaluate Equations (85) and (86) in two asymptotic regions: the near field
region ![]() , and the far field region
, and the far field region ![]() . In the near field region,
. In the near field region,

![$\displaystyle [\rho] \simeq \rho + \frac{\partial\rho}{\partial t} \,(t_r-t) + \frac{1}{2} \frac{\partial^{\,2} \rho}{\partial t^{\,2}}\,(t_r -t )^2+\cdots,$](img239.png)
![$\displaystyle [\rho] \simeq \rho - \frac{\partial \rho}{\partial t} \frac{R}{c}...
... \frac{\partial^{\,2} \rho}{\partial t^{\,2}} \frac{R^{\,2}}{c^{\,2}} + \cdots.$](img240.png)
![]() , Equations (85) and (86) are dominated by the terms that
vary like
, Equations (85) and (86) are dominated by the terms that
vary like ![]() , so that
, so that
![$\displaystyle \simeq -\frac{1}{4\pi\,\epsilon_0}\int\frac{[\partial {\bf j}_\perp /\partial t]}{c^{\,2} \,R} \,dV',$](img248.png)
![$\displaystyle \simeq \frac{\mu_0}{4\pi} \int \frac{ [\partial {\bf j}_\perp/\partial t]\times {\bf R} } {c\,R^{\,2}}\,dV',$](img249.png)

![]() , do the fields get really complicated.
, do the fields get really complicated.