


Next: Group Velocity
Up: Wave Propagation in Uniform
Previous: Sommerfeld Precursor
Method of Stationary Phase
Equation (887) can be written in the form
 |
(909) |
where
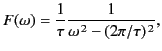 |
(910) |
and
 |
(911) |
Now, 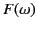 is a relatively slowly varying function
of
is a relatively slowly varying function
of  (except in the immediate vicinity of
the singular points,
(except in the immediate vicinity of
the singular points,
 ), whereas
the phase
), whereas
the phase
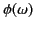 is generally large and rapidly varying.
The rapid oscillations of
is generally large and rapidly varying.
The rapid oscillations of
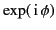 over most of the range
of integration means that the integrand averages to almost zero. Exceptions
to this cancellation rule occur only at points where
over most of the range
of integration means that the integrand averages to almost zero. Exceptions
to this cancellation rule occur only at points where
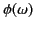 is stationary:
that is, where
is stationary:
that is, where
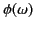 has an extremum. The integral can therefore be
estimated by finding all the points in the
has an extremum. The integral can therefore be
estimated by finding all the points in the  -plane where
-plane where
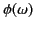 has a vanishing derivative,
evaluating (approximately) the integral in the neighborhood of each of
these points, and summing the contributions. This procedure is known as
the method of stationary phase.
has a vanishing derivative,
evaluating (approximately) the integral in the neighborhood of each of
these points, and summing the contributions. This procedure is known as
the method of stationary phase.
Suppose that
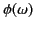 has a vanishing first derivative
at
has a vanishing first derivative
at
 . In the neighborhood of this point,
. In the neighborhood of this point,
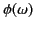 can be expanded as a Taylor series,
can be expanded as a Taylor series,
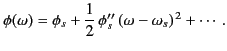 |
(912) |
Here, the subscript 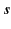 is used to indicate
is used to indicate 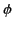 , or its
second derivative, evaluated at
, or its
second derivative, evaluated at
 , whereas
, whereas
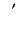 denotes a derivative with respect to
denotes a derivative with respect to  . Because
. Because 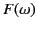 is slowly varying, the contribution to the integral from this
stationary phase point is approximately
is slowly varying, the contribution to the integral from this
stationary phase point is approximately
![$\displaystyle f_s \simeq F(\omega_s)\, {\rm e}^{\,{\rm i}\,\phi_s} \int_{\infty...
...ty} \exp\left[\frac{\rm i}{2}\,\phi_s'\,(\omega-\omega_s)^{\,2}\right] d\omega.$](img1907.png) |
(913) |
It is tacitly assumed that the stationary point lies on the real axis in
 -space, so that locally the integral along the contour
-space, so that locally the integral along the contour  is an
integral along the real axis in the direction of decreasing
is an
integral along the real axis in the direction of decreasing  .
The previous expression can be written in the form
.
The previous expression can be written in the form
![$\displaystyle f_s\simeq -F(\omega_s) \,{\rm e}^{\,{\rm i}\,\phi_s} \sqrt{\frac{...
...^\infty \left[ \cos(\pi\, t^{\,2}/2)+{\rm i}\,\sin(\pi \,t^{\,2}/2)\right]\,dt,$](img1908.png) |
(914) |
where
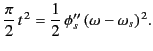 |
(915) |
The integrals in the previous expression are known as
Fresnel integrals,![[*]](footnote.png) and can be shown to take the values
and can be shown to take the values
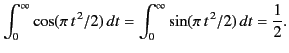 |
(916) |
It follows that
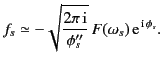 |
(917) |
It is easily demonstrated that the arc-length (in the  -plane) of the section of the integration contour
that makes a significant contribution to
-plane) of the section of the integration contour
that makes a significant contribution to 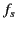 is of order
is of order
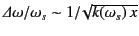 .
Thus, the arc-length is relatively short, provided that the wavelength of
the signal is much less than the distance it has propagated into the dispersive
medium.
If there is more than one point of stationary phase in the range
of integration then the integral is approximated as a sum of terms having the same form as the
previous one.
.
Thus, the arc-length is relatively short, provided that the wavelength of
the signal is much less than the distance it has propagated into the dispersive
medium.
If there is more than one point of stationary phase in the range
of integration then the integral is approximated as a sum of terms having the same form as the
previous one.
Integrals of the form (910) can be calculated exactly using the
method of steepest decent.![[*]](footnote.png) The stationary
phase approximation (918) agrees with the leading term of the
method of steepest decent (which is far more difficult to implement
than the method of stationary phase) provided that
The stationary
phase approximation (918) agrees with the leading term of the
method of steepest decent (which is far more difficult to implement
than the method of stationary phase) provided that
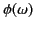 is
real (i.e., provided that
the stationary point lies on the real axis). If
is
real (i.e., provided that
the stationary point lies on the real axis). If 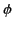 is complex, however, then the stationary phase
method can yield erroneous results. This suggests that the stationary
phase method is likely to break down when the extremum point
is complex, however, then the stationary phase
method can yield erroneous results. This suggests that the stationary
phase method is likely to break down when the extremum point
 approaches any poles or branch cuts in the
approaches any poles or branch cuts in the  -plane.
-plane.



Next: Group Velocity
Up: Wave Propagation in Uniform
Previous: Sommerfeld Precursor
Richard Fitzpatrick
2014-06-27

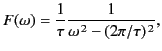
![]() has a vanishing first derivative
at
has a vanishing first derivative
at
![]() . In the neighborhood of this point,
. In the neighborhood of this point,
![]() can be expanded as a Taylor series,
can be expanded as a Taylor series,
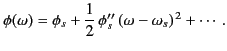
![$\displaystyle f_s \simeq F(\omega_s)\, {\rm e}^{\,{\rm i}\,\phi_s} \int_{\infty...
...ty} \exp\left[\frac{\rm i}{2}\,\phi_s'\,(\omega-\omega_s)^{\,2}\right] d\omega.$](img1907.png)
![$\displaystyle f_s\simeq -F(\omega_s) \,{\rm e}^{\,{\rm i}\,\phi_s} \sqrt{\frac{...
...^\infty \left[ \cos(\pi\, t^{\,2}/2)+{\rm i}\,\sin(\pi \,t^{\,2}/2)\right]\,dt,$](img1908.png)
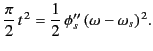
![[*]](footnote.png) and can be shown to take the values
and can be shown to take the values
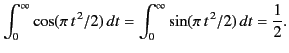
![[*]](footnote.png) The stationary
phase approximation (918) agrees with the leading term of the
method of steepest decent (which is far more difficult to implement
than the method of stationary phase) provided that
The stationary
phase approximation (918) agrees with the leading term of the
method of steepest decent (which is far more difficult to implement
than the method of stationary phase) provided that
![]() is
real (i.e., provided that
the stationary point lies on the real axis). If
is
real (i.e., provided that
the stationary point lies on the real axis). If ![]() is complex, however, then the stationary phase
method can yield erroneous results. This suggests that the stationary
phase method is likely to break down when the extremum point
is complex, however, then the stationary phase
method can yield erroneous results. This suggests that the stationary
phase method is likely to break down when the extremum point
![]() approaches any poles or branch cuts in the
approaches any poles or branch cuts in the ![]() -plane.
-plane.