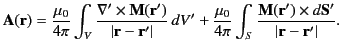Next: Uniformly Magnetized Sphere
Up: Magnetostatics in Magnetic Media
Previous: Boundary Conditions for and
Let us consider the magnetic field generated by a distribution of
permanent ferromagnets. Suppose that the magnets in question are
sufficiently ``hard'' that their magnetization is essentially independent
of the applied field for moderate field-strengths. Such magnets can be treated
as if they contain a fixed magnetization
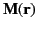 .
.
Let us assume that there are no true currents in the problem, so that
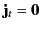 . Let us also assume that we are dealing with a
steady-state situation. Under these circumstances Equation (688) reduces to
. Let us also assume that we are dealing with a
steady-state situation. Under these circumstances Equation (688) reduces to
 |
(699) |
It follows that we can write
 |
(700) |
where 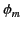 is called the magnetic scalar potential. Now,
we know that
is called the magnetic scalar potential. Now,
we know that
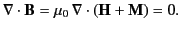 |
(701) |
Equations (701) and (702) combine to give
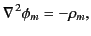 |
(702) |
where
 |
(703) |
Thus, the magnetostatic field,  , is determined by Poisson's
equation. We can think of
, is determined by Poisson's
equation. We can think of 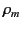 as an effective magnetic charge
density. Of course, this magnetic charge has no physical reality. We have
only introduced it in order to make the problem of the steady magnetic field
generated by a set of permanent magnets look formally the same as that
of the steady electric field generated by a distribution of charges.
as an effective magnetic charge
density. Of course, this magnetic charge has no physical reality. We have
only introduced it in order to make the problem of the steady magnetic field
generated by a set of permanent magnets look formally the same as that
of the steady electric field generated by a distribution of charges.
The unique solution of Poisson's equation, subject to sensible boundary conditions
at infinity, is well known (see Section 2.3):
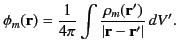 |
(704) |
This solution yields
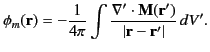 |
(705) |
If the magnetization field
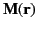 is well behaved and localized then
we can integrate by parts to obtain
is well behaved and localized then
we can integrate by parts to obtain
 |
(706) |
Now,
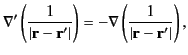 |
(707) |
so our expression for the magnetic potential can be written
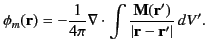 |
(708) |
Far from the region of non-vanishing magnetization, the potential reduces
to
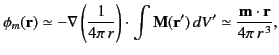 |
(709) |
where
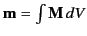 is the total magnetic moment of the distribution.
This is the scalar potential of a dipole. (See Sections 3.6 and 5.5.) Thus, an arbitrary localized
distribution of magnetization asymptotically produces a dipole magnetic field
whose strength is determined by the net
magnetic moment of the distribution.
is the total magnetic moment of the distribution.
This is the scalar potential of a dipole. (See Sections 3.6 and 5.5.) Thus, an arbitrary localized
distribution of magnetization asymptotically produces a dipole magnetic field
whose strength is determined by the net
magnetic moment of the distribution.
It is often a good approximation to treat the magnetization field
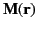 as a discontinuous quantity. In other words,
as a discontinuous quantity. In other words,
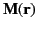 is specified throughout the ``hard'' ferromagnets
in question, and
suddenly falls to zero at the boundaries of these magnets. Integrating
Equation (704) over a Gaussian pill-box that straddles one of these boundaries
leads to the conclusion that there is an effective magnetic surface
charge density,
is specified throughout the ``hard'' ferromagnets
in question, and
suddenly falls to zero at the boundaries of these magnets. Integrating
Equation (704) over a Gaussian pill-box that straddles one of these boundaries
leads to the conclusion that there is an effective magnetic surface
charge density,
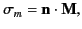 |
(710) |
on the surface of the ferromagnets, where 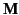 is the surface magnetization, and
is the surface magnetization, and 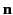 is a unit outward directed normal to the surface.
Under these circumstances, Equation (706) yields
is a unit outward directed normal to the surface.
Under these circumstances, Equation (706) yields
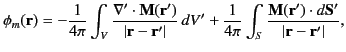 |
(711) |
where  represents the volume occupied by the magnets and
represents the volume occupied by the magnets and  is the
bounding surface to
is the
bounding surface to  . Here,
. Here, 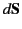 is an outward directed
element of
is an outward directed
element of  . It is clear that the right-hand side of Equation (712) consists of a volume integral
involving the volume magnetic charges
. It is clear that the right-hand side of Equation (712) consists of a volume integral
involving the volume magnetic charges
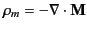 , and a surface integral involving the surface magnetic
charges
, and a surface integral involving the surface magnetic
charges
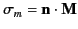 .
If the magnetization is uniform throughout the volume
.
If the magnetization is uniform throughout the volume  then the volume integral vanishes, and only the
surface integral makes a contribution.
then the volume integral vanishes, and only the
surface integral makes a contribution.
We can also write
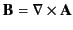 in order to satisfy
in order to satisfy
 automatically. It follows from
Equations (688) and (689) that
automatically. It follows from
Equations (688) and (689) that
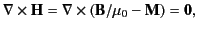 |
(712) |
which gives
 |
(713) |
because
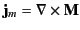 . The unique solution to
Equation (714), subject to sensible boundary conditions at infinity,
is well known:
. The unique solution to
Equation (714), subject to sensible boundary conditions at infinity,
is well known:
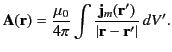 |
(714) |
Thus,
 |
(715) |
If the magnetization field is discontinuous, it is necessary to add
a surface integral to the previous expression. It is straightforward to
show that
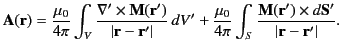 |
(716) |
It is clear that the previous expression consists of a volume integral
involving the volume magnetization currents
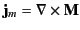 ,
and a surface integral involving the surface magnetization currents
,
and a surface integral involving the surface magnetization currents
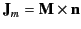 [see Equation (699)]. However, if the magnetization
field is uniform throughout
[see Equation (699)]. However, if the magnetization
field is uniform throughout  then only the surface integral makes
a contribution.
then only the surface integral makes
a contribution.



Next: Uniformly Magnetized Sphere
Up: Magnetostatics in Magnetic Media
Previous: Boundary Conditions for and
Richard Fitzpatrick
2014-06-27
![]() . Let us also assume that we are dealing with a
steady-state situation. Under these circumstances Equation (688) reduces to
. Let us also assume that we are dealing with a
steady-state situation. Under these circumstances Equation (688) reduces to
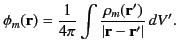

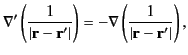
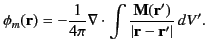
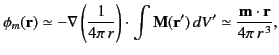
![]() as a discontinuous quantity. In other words,
as a discontinuous quantity. In other words,
![]() is specified throughout the ``hard'' ferromagnets
in question, and
suddenly falls to zero at the boundaries of these magnets. Integrating
Equation (704) over a Gaussian pill-box that straddles one of these boundaries
leads to the conclusion that there is an effective magnetic surface
charge density,
is specified throughout the ``hard'' ferromagnets
in question, and
suddenly falls to zero at the boundaries of these magnets. Integrating
Equation (704) over a Gaussian pill-box that straddles one of these boundaries
leads to the conclusion that there is an effective magnetic surface
charge density,
![]() in order to satisfy
in order to satisfy
![]() automatically. It follows from
Equations (688) and (689) that
automatically. It follows from
Equations (688) and (689) that