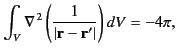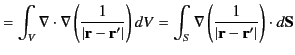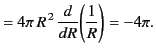Next: Solution of Inhomogeneous Wave
Up: Maxwell's Equations
Previous: Dirac Delta Function
Three-Dimensional Dirac Delta Function
The three-dimensional Dirac delta function,
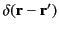 , has the property
, has the property
In addition, however, the function is singular at
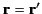 in such a manner
that
in such a manner
that
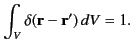 |
(22) |
Here,  is any volume that contains the point
is any volume that contains the point
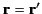 . (Also,
. (Also,  is an element of
is an element of  expressed in terms
of the components of
expressed in terms
of the components of  , but independent of the components of
, but independent of the components of  .) It follows that
.) It follows that
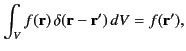 |
(23) |
where
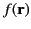 is an arbitrary function that is well behaved at
is an arbitrary function that is well behaved at
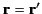 . It is also easy to see that
. It is also easy to see that
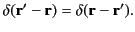 |
(24) |
We can show that
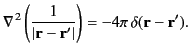 |
(25) |
(Here,
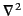 is a Laplacian operator expressed in terms of the components of
is a Laplacian operator expressed in terms of the components of  , but independent of the
components of
, but independent of the
components of  .)
We must first prove that
.)
We must first prove that
in accordance with Equation (21). If
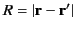 then this is equivalent to showing that
then this is equivalent to showing that
![$\displaystyle \frac{1}{R^{\,2}}\,\frac{d}{dR}\!\left[R^{\,2}\,\frac{d}{dR}\!\left(\frac{1}{R}\right)\right]=0$](img99.png) |
(27) |
for  , which is indeed the case. (Here,
, which is indeed the case. (Here, 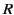 is treated as a radial spherical coordinate.) Next, we must show that
is treated as a radial spherical coordinate.) Next, we must show that
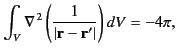 |
(28) |
in accordance with Equations (22) and (25).
Suppose that  is a spherical surface, of radius
is a spherical surface, of radius 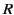 , centered on
, centered on
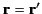 . Making use of the
definition
. Making use of the
definition
 , as well as the divergence theorem, we can write
, as well as the divergence theorem, we can write
(Here, 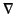 is a gradient operator expressed in terms of the components of
is a gradient operator expressed in terms of the components of  , but independent of the components
of
, but independent of the components
of  . Likewise,
. Likewise, 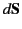 is a surface element involving the components of
is a surface element involving the components of  , but independent
of the components of
, but independent
of the components of  .)
Finally, if
.)
Finally, if  is deformed into a general surface (without crossing the point
is deformed into a general surface (without crossing the point
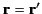 ) then the value of the
volume integral is unchanged, as a consequence of Equation (26).
Hence, we have demonstrated the validity of Equation (25).
) then the value of the
volume integral is unchanged, as a consequence of Equation (26).
Hence, we have demonstrated the validity of Equation (25).



Next: Solution of Inhomogeneous Wave
Up: Maxwell's Equations
Previous: Dirac Delta Function
Richard Fitzpatrick
2014-06-27
![$\displaystyle \frac{1}{R^{\,2}}\,\frac{d}{dR}\!\left[R^{\,2}\,\frac{d}{dR}\!\left(\frac{1}{R}\right)\right]=0$](img99.png)