Dirac Delta Function

The Dirac delta function, 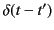$\delta(t-t')$ , has the property

$$\delta(t-t') =0 \mbox{\hspace{0.5cm}for\hspace{0.5cm}$t\neq t'$} .$$ (17)

In addition, however, the function is singular at 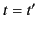$t=t'$ in such a manner that

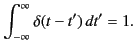$$\int_{-\infty}^\infty \delta (t-t')\,dt' = 1.$$ (18)

It follows that

$$\int_{-\infty}^\infty f(t)\,\delta(t-t')\,dt' = f(t),$$ (19)

where $f(t)$ is an arbitrary function that is well behaved at 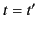$t=t'$ . It is also easy to see that

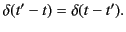$$\delta(t'-t) = \delta(t-t').$$ (20)