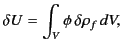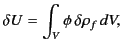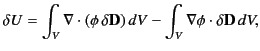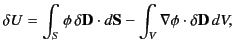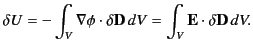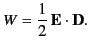Next: Force Density Within Dielectric
Up: Electrostatics in Dielectric Media
Previous: Boundary Value Problems with
Consider a system of free charges embedded in a dielectric
medium. The increase in the total energy when a small
amount of free charge
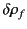 is added to the system
is given by
is added to the system
is given by
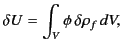 |
(559) |
where the integral is taken over all space,
and
 is the
electrostatic potential.
Here, it is assumed that the original charges and the dielectric are
held fixed, so that no mechanical work is performed.
It follows from Equation (501) that
is the
electrostatic potential.
Here, it is assumed that the original charges and the dielectric are
held fixed, so that no mechanical work is performed.
It follows from Equation (501) that
 |
(560) |
where
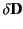 is the change in the electric displacement associated
with the charge increment. Now, the above equation can also be written
is the change in the electric displacement associated
with the charge increment. Now, the above equation can also be written
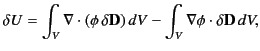 |
(561) |
giving
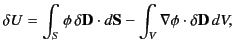 |
(562) |
where use has been made of the divergence theorem. If the dielectric medium
is of finite
spatial extent then we can neglect the surface term to give
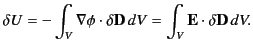 |
(563) |
This energy increment cannot be integrated unless  is a known
function of
is a known
function of 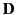 . Let us adopt the conventional approach, and assume that
. Let us adopt the conventional approach, and assume that
 , where the dielectric constant
, where the dielectric constant
 is independent of the electric field. The
change in energy associated with taking the displacement field from
zero to
is independent of the electric field. The
change in energy associated with taking the displacement field from
zero to
 at all points in space is given by
at all points in space is given by
 |
(564) |
or
 |
(565) |
which reduces to
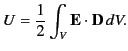 |
(566) |
Thus, the electrostatic energy density inside a dielectric is given by
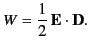 |
(567) |
This is a standard result that is often quoted in textbooks. Nevertheless,
it is important to realize that the above formula is only valid in dielectric
media
in which
the electric displacement, 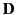 , varies linearly with the
electric field,
, varies linearly with the
electric field,  .
.



Next: Force Density Within Dielectric
Up: Electrostatics in Dielectric Media
Previous: Boundary Value Problems with
Richard Fitzpatrick
2014-06-27