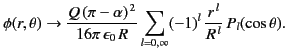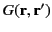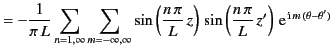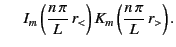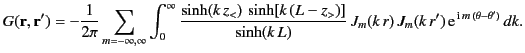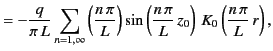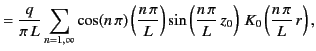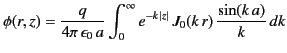Next: Electrostatics in Dielectric Media
Up: Potential Theory
Previous: Poisson's Equation in Cylindrical
- Two concentric spheres have radii
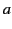 ,
,  (
(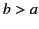 ) and are each divided into two hemispheres
by the same horizontal plane. The upper hemisphere of the inner sphere and the lower hemisphere
of the outer sphere are maintained at potential
) and are each divided into two hemispheres
by the same horizontal plane. The upper hemisphere of the inner sphere and the lower hemisphere
of the outer sphere are maintained at potential  . The other hemispheres are at zero potential.
Demonstrate that the potential in the region
. The other hemispheres are at zero potential.
Demonstrate that the potential in the region
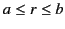 can be written
can be written
where
Here, 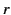 ,
,  ,
, 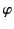 are conventional spherical coordinates whose origin coincides with the common center of the spheres, and are such that the dividing plane corresponds to
are conventional spherical coordinates whose origin coincides with the common center of the spheres, and are such that the dividing plane corresponds to
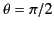 .
.
- A spherical surface of radius
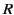 has charge uniformly distributed over its surface with
density
has charge uniformly distributed over its surface with
density
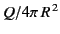 , except for a spherical cap at the north pole, defined by the cone
, except for a spherical cap at the north pole, defined by the cone
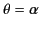 . Here,
. Here, 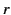 ,
,  ,
, 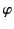 are conventional spherical
coordinates whose origin coincides with the center of the surface.
are conventional spherical
coordinates whose origin coincides with the center of the surface.
- Show that the potential inside the spherical surface can be expressed as
where
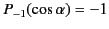 .
.
- Show that the electric field at the origin is
- Show that in the limit
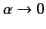 ,
,
- Show that in the limit
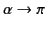 ,
,
- The Dirichlet Green's function for the unbounded space between planes at
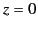 and
and 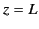 allows a
discussion of a point charge, or a distribution of charge, between parallel conducting planes held at zero potential.
allows a
discussion of a point charge, or a distribution of charge, between parallel conducting planes held at zero potential.
- Using cylindrical coordinates, show that one form of the Green's function is
- Show that an alternative form of the Green's function is
- From the results of the previous exercise, show that the potential due to a point charge
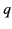 placed between two infinite parallel conducting
planes held at zero potential can be written as
placed between two infinite parallel conducting
planes held at zero potential can be written as
where the planes are at 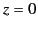 and
and 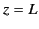 , and the charge is on the
, and the charge is on the  -axis at
-axis at 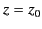 . Show that induced surface charge densities on the
lower and upper planes are
. Show that induced surface charge densities on the
lower and upper planes are
respectively.
- Show that the potential due to a conducting disk of radius
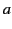 carrying a charge
carrying a charge 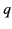 is
is
in cylindrical coordinates (whose origin coincides with the center of the disk, and whose symmetry axis coincides with that of the disk.)
- A conducting spherical shell of radius
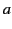 is placed in a uniform electric field
is placed in a uniform electric field  . Show that the force tending to
separate two halves of the sphere across a diametral plane perpendicular to
. Show that the force tending to
separate two halves of the sphere across a diametral plane perpendicular to  is given by
is given by



Next: Electrostatics in Dielectric Media
Up: Potential Theory
Previous: Poisson's Equation in Cylindrical
Richard Fitzpatrick
2014-06-27
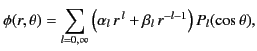
![$\displaystyle = \frac{V}{2}\left[\frac{a^{\,l+1}-(-1)^l\,b^{\,l+1}}{a^{\,2\,l+1}-b^{\,2\,l+1}}\right]\left[P_{l-1}(0)-P_{l+1}(0)\right],$](img1032.png)
![$\displaystyle = \frac{V}{2}\left[\frac{a^{-l}-(-1)^l\,b^{-l}}{a^{-2\,l-1}-b^{-2\,l-1}}\right]\left[P_{l-1}(0)-P_{l+1}(0)\right].$](img1034.png)
![$\displaystyle \phi(r,\theta) = \frac{Q}{8\pi\,\epsilon_0}\sum_{l=0,\infty}\frac...
...\alpha)-P_{l-1}(\cos\alpha)\right]\frac{r^{\,l}}{R^{\,l+1}}\,
P_l(\cos\theta),
$](img1038.png)
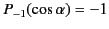 .
.

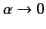 ,
,
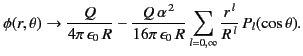
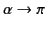 ,
,