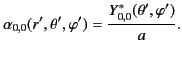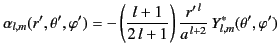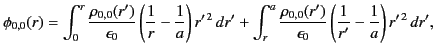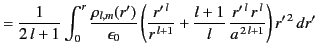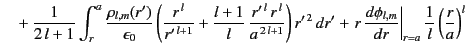Next: Laplace's Equation in Cylindrical
Up: Potential Theory
Previous: Dirichlet Problem in Spherical
According to Section 2.10, the solution to the Newmann problem, in which the charge density is specified
within some volume 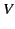 , and the normal derivative of the potential given on the bounding surface
, and the normal derivative of the potential given on the bounding surface 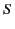 ,
takes the form
,
takes the form
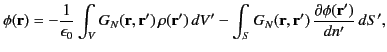 |
(382) |
where the Newmann Green's function is
written
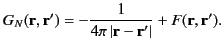 |
(383) |
Here,
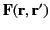 is solution of Laplace's equation (i.e.,
is solution of Laplace's equation (i.e.,
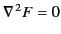 ) which is chosen so as to ensure that
) which is chosen so as to ensure that
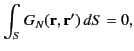 |
(384) |
and
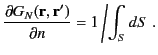 |
(385) |
The latter constraint holds when 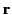 (or
(or 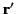 ) lies on
) lies on 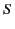 . Note that we have chosen the arbitrary constant to which the potential
. Note that we have chosen the arbitrary constant to which the potential
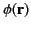 is undetermined such that
is undetermined such that
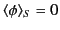 .
It again follows from Sections 3.4 and 3.5
that
.
It again follows from Sections 3.4 and 3.5
that
where the
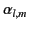 and the
and the
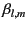 are chosen in such a manner that the constraints (385) and (386) are satisfied.
are chosen in such a manner that the constraints (385) and (386) are satisfied.
As a specific example, suppose that the volume 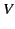 lies inside the spherical surface
lies inside the spherical surface 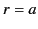 .
The physical constraint that the Green's function remain finite at
.
The physical constraint that the Green's function remain finite at 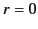 implies that the
implies that the
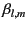 are all zero.
Applying the constraint (385) at
are all zero.
Applying the constraint (385) at 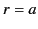 , we get
, we get
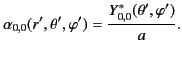 |
(387) |
Similarly, the constraint (386) leads to
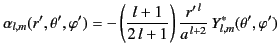 |
(388) |
for 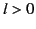 .
Hence, the unique Green's function for the problem becomes
.
Hence, the unique Green's function for the problem becomes
Finally, expanding
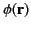 and
and
 in the forms (378) and (379), respectively, Equations (383) and
(390) yield
in the forms (378) and (379), respectively, Equations (383) and
(390) yield
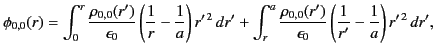 |
(390) |
and
for 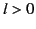 .
.



Next: Laplace's Equation in Cylindrical
Up: Potential Theory
Previous: Dirichlet Problem in Spherical
Richard Fitzpatrick
2014-06-27
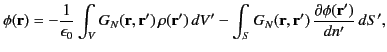
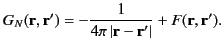
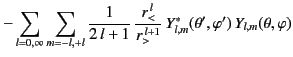
![$\displaystyle + \sum_{l=0,\infty}\sum_{m=-l,+l}\left[\alpha_{l,m}(r',\theta',\v...
...rac{\beta_{l,m}(r',\theta',\varphi')}{r^{\,l+1}}\right]Y_{l,m}(\theta,\varphi),$](img834.png)
![]() lies inside the spherical surface
lies inside the spherical surface ![]() .
The physical constraint that the Green's function remain finite at
.
The physical constraint that the Green's function remain finite at ![]() implies that the
implies that the
![]() are all zero.
Applying the constraint (385) at
are all zero.
Applying the constraint (385) at ![]() , we get
, we get