


Next: Laplace's Equation in Spherical
Up: Potential Theory
Previous: Associated Legendre Functions
Spherical Harmonics
The spherical harmonics,
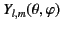 , are the angular portions of the global
solutions to Laplace's equation in standard spherical coordinates,
, are the angular portions of the global
solutions to Laplace's equation in standard spherical coordinates, 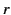 ,
,  ,
, 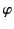 . Here,
. Here,  is a non-negative
integer (known as the degree), and
is a non-negative
integer (known as the degree), and  is an integer (known as the order) lying in the range
is an integer (known as the order) lying in the range
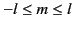 . The spherical
harmonics are well behaved and single valued functions that satisfy the
differential equation
. The spherical
harmonics are well behaved and single valued functions that satisfy the
differential equation
 |
(307) |
and take the form![[*]](footnote.png)
![$\displaystyle Y_{l,m}(\theta,\varphi)= \left[\frac{(2\,l+1)\,(l-m)!}{4\pi\,(l+m)!}\right]^{1/2}\,P_l^{\,m}(\cos\theta)\,{\rm e}^{\,{\rm i}\,m\,\varphi}.$](img709.png) |
(308) |
It follows from Equation (295) that
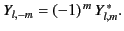 |
(309) |
The
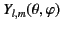 satisfy the orthonormality constraint
satisfy the orthonormality constraint
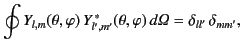 |
(310) |
where
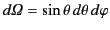 is a an element of solid angle, and the integral is taken
over all solid angle.
Note that the spherical harmonics form a complete set of angular functions.
is a an element of solid angle, and the integral is taken
over all solid angle.
Note that the spherical harmonics form a complete set of angular functions.
All of the spherical harmonics of degree less than 3 are listed below:
Consider two spherical coordinate systems, 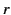 ,
,  ,
, 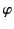 and
and 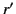 ,
, 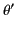 ,
, 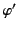 , whose origins coincide, but
whose polar axes subtend an angle
, whose origins coincide, but
whose polar axes subtend an angle  with respect to one another. It follows that
with respect to one another. It follows that
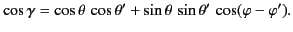 |
(320) |
Moreover, the so-called addition theorem for spherical harmonics states that![[*]](footnote.png)
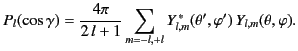 |
(321) |



Next: Laplace's Equation in Spherical
Up: Potential Theory
Previous: Associated Legendre Functions
Richard Fitzpatrick
2014-06-27
![[*]](footnote.png)
![]() ,
, ![]() ,
, ![]() and
and ![]() ,
, ![]() ,
, ![]() , whose origins coincide, but
whose polar axes subtend an angle
, whose origins coincide, but
whose polar axes subtend an angle ![]() with respect to one another. It follows that
with respect to one another. It follows that
![[*]](footnote.png)