![$\displaystyle = \frac{1}{4\pi\,\epsilon_0} \int \frac{[\rho({\bf r}')]}{\vert{\bf r}- {\bf r}'\vert}\,dV',$](img3740.png) |
(1746) | |
![$\displaystyle = \frac{\mu_0}{4\pi} \int \frac{[{\bf j}({\bf r}')]}{\vert{\bf r}- {\bf r}'\vert}\,dV'.$](img3741.png) |
(1747) |
![$\displaystyle = \frac{1}{4\pi\,\epsilon_0} \int \frac{[\rho({\bf r}')]}{\vert{\bf r}- {\bf r}'\vert}\,dV',$](img3740.png) |
(1746) | |
![$\displaystyle = \frac{\mu_0}{4\pi} \int \frac{[{\bf j}({\bf r}')]}{\vert{\bf r}- {\bf r}'\vert}\,dV'.$](img3741.png) |
(1747) |
But, does the right-hand side of Equation (1750) really transform as a
contravariant 4-vector? This is not a trivial question, because volume
integrals in 3-space
are not, in general, Lorentz invariant due to the length contraction
effect. However, the integral in Equation (1750) is not a straightforward
volume integral, because the integrand is evaluated at the retarded time.
In fact, the integral is best regarded as an integral over events in
space-time. The events that enter the integral are those which intersect
a spherical light wave launched from the event ![]() and evolved backwards in
time. In other words, the events occur before the event
and evolved backwards in
time. In other words, the events occur before the event ![]() , and have
zero interval with respect to
, and have
zero interval with respect to ![]() . It is clear that observers in all
inertial frames will, at least, agree on which events are to be included
in the integral, because both the interval between events, and the absolute
order in which events occur, are invariant under a
general Lorentz transformation.
. It is clear that observers in all
inertial frames will, at least, agree on which events are to be included
in the integral, because both the interval between events, and the absolute
order in which events occur, are invariant under a
general Lorentz transformation.
We shall now demonstrate that all observers obtain the same value of
![]() for each elementary contribution to the integral. Suppose
that
for each elementary contribution to the integral. Suppose
that ![]() and
and ![]() are two inertial frames in the standard configuration.
Let unprimed and primed symbols denote corresponding quantities in
are two inertial frames in the standard configuration.
Let unprimed and primed symbols denote corresponding quantities in
![]() and
and ![]() , respectively.
Let us assign coordinates
, respectively.
Let us assign coordinates
![]() to
to ![]() , and
, and
![]() to the
retarded event
to the
retarded event ![]() for which
for which ![]() and
and ![]() are evaluated. Using the
standard Lorentz transformation, (1643)-(1646), the fact that the interval
between events
are evaluated. Using the
standard Lorentz transformation, (1643)-(1646), the fact that the interval
between events ![]() and
and ![]() is zero, and the fact that both
is zero, and the fact that both ![]() and
and
![]() are negative, we obtain
are negative, we obtain
| (1749) |
We now know the transformation for ![]() . What about the transformation for
. What about the transformation for
![]() ? We might be tempted to set
? We might be tempted to set
![]() , according to the
usual length contraction rule. However, this is incorrect. The contraction
by a factor
, according to the
usual length contraction rule. However, this is incorrect. The contraction
by a factor ![]() only applies if the whole of the volume is
measured at the same time, which is not the case in the present
problem. Now, the dimensions of
only applies if the whole of the volume is
measured at the same time, which is not the case in the present
problem. Now, the dimensions of ![]() along the
along the ![]() - and
- and ![]() -axes
are the same in both
-axes
are the same in both ![]() and
and ![]() , according to Equations (1643)-(1646).
For the
, according to Equations (1643)-(1646).
For the ![]() -dimension these equations give
-dimension these equations give
![]() .
The extremities of
.
The extremities of ![]() are measured at times differing by
are measured at times differing by ![]() , where
, where
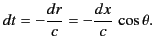 |
(1751) |
| (1752) |
Thus, ![]() is an invariant and, therefore,
is an invariant and, therefore,
![]() is
a contravariant 4-vector. For linear transformations, such as a
general Lorentz transformation, the result of adding 4-tensors
evaluated at different 4-points is itself a 4-tensor. It follows that the
right-hand side of Equation (1750) is indeed a contravariant 4-vector. Thus,
this 4-vector equation can be properly regarded as the solution to the
4-vector wave equation (1739).
is
a contravariant 4-vector. For linear transformations, such as a
general Lorentz transformation, the result of adding 4-tensors
evaluated at different 4-points is itself a 4-tensor. It follows that the
right-hand side of Equation (1750) is indeed a contravariant 4-vector. Thus,
this 4-vector equation can be properly regarded as the solution to the
4-vector wave equation (1739).