A tensor of rank ![]() in an
in an ![]() -dimensional space possesses
-dimensional space possesses ![]() components
which are, in general, functions of position in that space. A tensor of
rank zero has one component,
components
which are, in general, functions of position in that space. A tensor of
rank zero has one component, ![]() , and is called a scalar. A tensor
of rank one has
, and is called a scalar. A tensor
of rank one has ![]() components,
components,
![]() , and is called
a vector. A tensor of rank two has
, and is called
a vector. A tensor of rank two has ![]() components, which can be
exhibited in matrix format. Unfortunately, there is no convenient way of
exhibiting a higher rank tensor. Consequently, tensors are usually
represented by a typical component: for instance,
the tensor
components, which can be
exhibited in matrix format. Unfortunately, there is no convenient way of
exhibiting a higher rank tensor. Consequently, tensors are usually
represented by a typical component: for instance,
the tensor ![]() (rank 3), or the tensor
(rank 3), or the tensor ![]() (rank 4),
et cetera. The suffixes
(rank 4),
et cetera. The suffixes
![]() are always understood to range from
1 to
are always understood to range from
1 to ![]() .
.
For reasons that will become apparent later on, we shall
represent tensor components using both
superscripts and subscripts. Thus, a typical tensor might look like
![]() (rank 2), or
(rank 2), or ![]() (rank 2), et cetera. It is convenient to
adopt the Einstein summation convention. Namely, if any suffix appears twice
in a given term, once as a subscript and once as a superscript, a summation
over that suffix (from 1 to
(rank 2), et cetera. It is convenient to
adopt the Einstein summation convention. Namely, if any suffix appears twice
in a given term, once as a subscript and once as a superscript, a summation
over that suffix (from 1 to ![]() ) is implied.
) is implied.
To distinguish between various different coordinate systems, we shall use primed
and multiply primed suffixes. A first system of coordinates
![]() can then be denoted by
can then be denoted by ![]() , a second
system
, a second
system
![]() by
by ![]() , et cetera.
Similarly, the general components of a tensor in various coordinate
systems are distinguished by their suffixes. Thus, the components
of some third rank tensor are denoted
, et cetera.
Similarly, the general components of a tensor in various coordinate
systems are distinguished by their suffixes. Thus, the components
of some third rank tensor are denoted ![]() in the
in the ![]() system,
by
system,
by
![]() in the
in the ![]() system, et cetera.
system, et cetera.
When making a coordinate transformation from one set of coordinates,
![]() , to another,
, to another, ![]() , it is assumed that the transformation is
non-singular. In other words, the equations that express the
, it is assumed that the transformation is
non-singular. In other words, the equations that express the ![]() in
terms of the
in
terms of the ![]() can be inverted to express the
can be inverted to express the ![]() in terms
of the
in terms
of the ![]() . It is also assumed that the functions specifying a
transformation are differentiable. It is convenient to
write
. It is also assumed that the functions specifying a
transformation are differentiable. It is convenient to
write
| (1664) | ||
| (1665) |
| (1666) |
The formal definition of a tensor is as follows:
When an entity is described as a tensor it is generally understood that it behaves as a tensor under all non-singular differentiable transformations of the relevant coordinates. An entity that only behaves as a tensor under a certain subgroup of non-singular differentiable coordinate transformations is called a qualified tensor, because its name is conventionally qualified by an adjective recalling the subgroup in question. For instance, an entity that only exhibits tensor behavior under Lorentz transformations is called a Lorentz tensor, or, more commonly, a 4-tensor.
When applied to a tensor of rank zero (a scalar), the previous definitions
imply that ![]() . Thus, a scalar is a function of position
only, and is independent of the coordinate system. A scalar is often
termed an invariant.
. Thus, a scalar is a function of position
only, and is independent of the coordinate system. A scalar is often
termed an invariant.
The main theorem of tensor calculus is as follows:
If two tensors of the same type are equal in one coordinate system then they are equal in all coordinate systems.
The simplest example of a contravariant vector (tensor of rank one)
is provided by the differentials of the coordinates,
![]() , because
, because
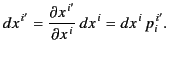 |
(1670) |
The simplest example of a covariant vector is provided by the gradient
of a function of position
![]() , because if we
write
, because if we
write
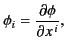 |
(1671) |
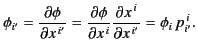 |
(1672) |
An important example of a mixed second-rank tensor is provided by the Kronecker delta introduced previously, because
| (1673) |
Tensors of the same type can be added or subtracted to form new
tensors. Thus, if ![]() and
and ![]() are tensors, then
are tensors, then
![]() is a tensor of the same type. Note that
the sum of tensors at different points in space is not a tensor if
the
is a tensor of the same type. Note that
the sum of tensors at different points in space is not a tensor if
the ![]() 's are position dependent. However, under linear coordinate
transformations the
's are position dependent. However, under linear coordinate
transformations the ![]() 's are constant, so the sum of tensors at different points
behaves as a tensor under this particular type of coordinate transformation.
's are constant, so the sum of tensors at different points
behaves as a tensor under this particular type of coordinate transformation.
If ![]() and
and ![]() are tensors, then
are tensors, then
![]() is a tensor of the type indicated by the suffixes. The
process illustrated by this example is called outer multiplication
of tensors.
is a tensor of the type indicated by the suffixes. The
process illustrated by this example is called outer multiplication
of tensors.
Tensors can also be combined by inner multiplication, which implies
at least one dummy suffix link. Thus,
![]() and
and
![]() are tensors of the type indicated by the suffixes.
are tensors of the type indicated by the suffixes.
Finally, tensors can be formed by contraction from tensors of
higher rank. Thus, if
![]() is a tensor then
is a tensor then
![]() and
and
![]() are tensors of the
type indicated by the suffixes. The most important type of contraction
occurs when no free suffixes remain: the result is a scalar. Thus,
are tensors of the
type indicated by the suffixes. The most important type of contraction
occurs when no free suffixes remain: the result is a scalar. Thus,
![]() is a scalar provided that
is a scalar provided that ![]() is a tensor.
is a tensor.
Although we cannot usefully divide tensors, one by another, an entity
like ![]() in the equation
in the equation
![]() , where
, where ![]() and
and ![]() are tensors, can be formally regarded as the quotient of
are tensors, can be formally regarded as the quotient of ![]() and
and
![]() . This gives the name to a particularly useful rule for
recognizing tensors, the quotient rule. This rule states that
if a set of components, when combined by a given type of multiplication
with all tensors of a given type yields a tensor, then the set is
itself a tensor. In other words, if the product
. This gives the name to a particularly useful rule for
recognizing tensors, the quotient rule. This rule states that
if a set of components, when combined by a given type of multiplication
with all tensors of a given type yields a tensor, then the set is
itself a tensor. In other words, if the product
![]() transforms like a tensor for all tensors
transforms like a tensor for all tensors
![]() then it follows that
then it follows that ![]() is a tensor.
is a tensor.
Let
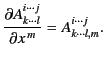 |
(1674) |
| (1675) |
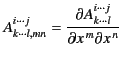 |
(1676) |
So far, the space to which the coordinates ![]() refer has been without
structure. We can impose a structure on it by defining the distance
between all pairs of neighboring points by means of a metric,
refer has been without
structure. We can impose a structure on it by defining the distance
between all pairs of neighboring points by means of a metric,
The elements of the inverse of the matrix ![]() are denoted
by
are denoted
by ![]() . These elements are uniquely defined by the equations
. These elements are uniquely defined by the equations
| (1678) |
The tensors ![]() and
and ![]() allow us to introduce the important
operations of raising and lowering suffixes. These operations
consist of forming inner products of a given tensor with
allow us to introduce the important
operations of raising and lowering suffixes. These operations
consist of forming inner products of a given tensor with ![]() or
or ![]() . For example, given a contravariant vector
. For example, given a contravariant vector
![]() , we define its covariant components
, we define its covariant components ![]() by the equation
by the equation
| (1679) |
| (1680) |
| (1681) |
By analogy with Euclidian space, we define the squared magnitude
![]() of a vector
of a vector ![]() with respect to the metric
with respect to the metric
![]() by the equation
by the equation
| (1682) |
| (1683) |
Finally, let us consider differentiation with respect to an invariant distance,
![]() . The vector
. The vector
![]() is a contravariant tensor, because
is a contravariant tensor, because
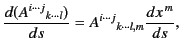 |
(1685) |