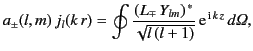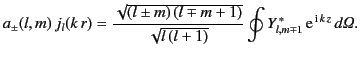Next: Mie Scattering
Up: Multipole Expansion
Previous: Radiation from Linear Centre-Fed
In discussing the scattering or absorption of electromagnetic radiation
by localized systems, it is useful to be able to express
a plane electromagnetic wave as a superposition of spherical waves.
Consider, first of all, the expansion of a scalar plane wave as a set of scalar
spherical waves. This expansion is conveniently
obtained from the expansion
(1517) for the Green's function of the scalar Helmholtz equation.
Let us take the limit
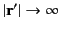 of this equation.
We can make the substitution
of this equation.
We can make the substitution
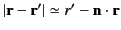 on the left-hand-side, where
on the left-hand-side, where
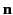 is a unit vector pointing in the direction of
is a unit vector pointing in the direction of  .
On the right-hand side,
.
On the right-hand side, 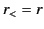 and
and 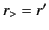 . Furthermore, we can use
the asymptotic form (1432) for
. Furthermore, we can use
the asymptotic form (1432) for
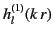 . Thus, we obtain
. Thus, we obtain
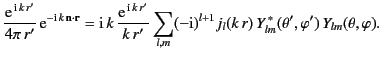 |
(1566) |
Canceling the factor
 on either side of the above equation,
and taking the complex conjugate, we get the following expansion for
a scalar plane wave,
on either side of the above equation,
and taking the complex conjugate, we get the following expansion for
a scalar plane wave,
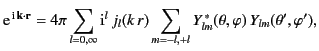 |
(1567) |
where 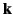 is a wavevector with the spherical coordinates
is a wavevector with the spherical coordinates
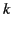 ,
, 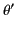 ,
, 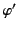 . The well-known addition theorem
for the spherical harmonics states that
. The well-known addition theorem
for the spherical harmonics states that
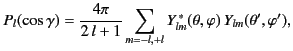 |
(1568) |
where  is the angle subtended between the vectors
is the angle subtended between the vectors  and
and 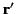 . Consequently,
. Consequently,
 |
(1569) |
It follows from Equations (1569) and (1570) that
 |
(1570) |
or
 |
(1571) |
because
 |
(1572) |
Let us now make an equivalent expansion for a circularly polarized plane
wave incident along the  -axis:
-axis:
Because the plane wave is finite everywhere (including the origin), its
multipole expansion (1479)-(1480) can only involve the well-behaved
radial eigenfunctions  . Thus,
. Thus,
To determine the coefficients
 and
and
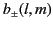 , we make
use of a slight generalization of the standard orthogonality properties
(1477)-(1478) of the vector spherical harmonics:
, we make
use of a slight generalization of the standard orthogonality properties
(1477)-(1478) of the vector spherical harmonics:
The first of these follows directly from Equation (1477). The second
follows from Equations (1442), (1478), (1486), and the identity
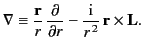 |
(1579) |
The coefficients
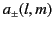 and
and
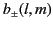 are obtained by taking
the scalar product of Equations (1577)-(1578) with
are obtained by taking
the scalar product of Equations (1577)-(1578) with
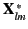 and
integrating over all solid angle, making use of the orthogonality
relations (1579)-(1580). This yields
and
integrating over all solid angle, making use of the orthogonality
relations (1579)-(1580). This yields
Substitution of Equations (1476) and (1577) into Equation (1582) gives
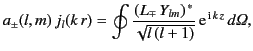 |
(1582) |
where the operators  are defined in Equations (1439)-(1440). Making use of
Equations (1444)-(1446), the above expression reduces to
are defined in Equations (1439)-(1440). Making use of
Equations (1444)-(1446), the above expression reduces to
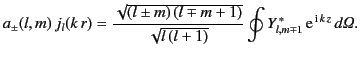 |
(1583) |
If the expansion (1573) is substituted for
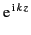 , and use is made of the orthogonality properties
of the spherical harmonics,
then we obtain the result
, and use is made of the orthogonality properties
of the spherical harmonics,
then we obtain the result
 |
(1584) |
It is clear from Equations (1576) and (1583) that
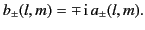 |
(1585) |
Thus, the general expansion of a circularly polarized plane wave takes
the form
The expansion for a linearly polarized plane wave is easily obtained
by taking
the appropriate linear combination of the above two expansions.



Next: Mie Scattering
Up: Multipole Expansion
Previous: Radiation from Linear Centre-Fed
Richard Fitzpatrick
2014-06-27
![]() of this equation.
We can make the substitution
of this equation.
We can make the substitution
![]() on the left-hand-side, where
on the left-hand-side, where
![]() is a unit vector pointing in the direction of
is a unit vector pointing in the direction of ![]() .
On the right-hand side,
.
On the right-hand side, ![]() and
and ![]() . Furthermore, we can use
the asymptotic form (1432) for
. Furthermore, we can use
the asymptotic form (1432) for
![]() . Thus, we obtain
. Thus, we obtain
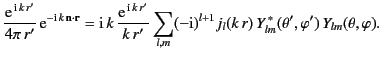


![]() -axis:
-axis:
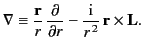
![]() and
and
![]() are obtained by taking
the scalar product of Equations (1577)-(1578) with
are obtained by taking
the scalar product of Equations (1577)-(1578) with
![]() and
integrating over all solid angle, making use of the orthogonality
relations (1579)-(1580). This yields
and
integrating over all solid angle, making use of the orthogonality
relations (1579)-(1580). This yields