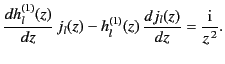Next: Sources of Multipole Radiation
Up: Multipole Expansion
Previous: Properties of Multipole Fields
The inhomogeneous Helmholtz wave equation is conveniently solved by means of a Green's function,
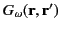 , that satisfies
, that satisfies
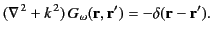 |
(1506) |
The solution of this equation, subject to the Sommerfeld radiation
condition, which ensures that sources radiate waves instead of absorbing
them, is written
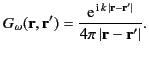 |
(1507) |
(See Chapter 1.)
As is well known, the spherical harmonics satisfy the completeness relation
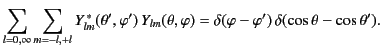 |
(1508) |
Now, the three-dimensional delta function can be written
 |
(1509) |
It follows that
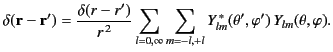 |
(1510) |
Let us expand the Green's function in the form
 |
(1511) |
Substitution of this expression into Equation (1508) yields
![$\displaystyle \left[\frac{d^{\,2}}{dr^{\,2}} +\frac{2}{r}\frac{d}{dr}+k^{\,2} -\frac{l\,(l+1)}{r^{\,2}}\right] g_l = - \frac{\delta(r-r')}{r^{\,2}}.$](img3180.png) |
(1512) |
The appropriate boundary conditions are that 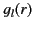 be finite at the
origin, and correspond to an outgoing wave at infinity
(i.e.,
be finite at the
origin, and correspond to an outgoing wave at infinity
(i.e.,
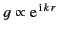 in the limit
in the limit
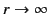 ). The solution of the above equation that
satisfies these boundary conditions is
). The solution of the above equation that
satisfies these boundary conditions is
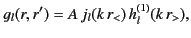 |
(1513) |
where 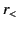 and
and 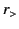 are the greater and the lesser of
are the greater and the lesser of
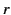 and
and 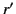 , respectively. The appropriate discontinuity
in slope at
, respectively. The appropriate discontinuity
in slope at 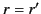 is assured if
is assured if
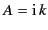 ,
because
,
because
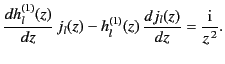 |
(1514) |
Thus, the expansion of the Green's function becomes
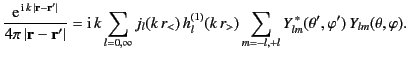 |
(1515) |
This is a particularly useful result,
as we shall discover, because it easily allows
us to express the general
solution of the inhomogeneous wave equation as a multipole expansion.



Next: Sources of Multipole Radiation
Up: Multipole Expansion
Previous: Properties of Multipole Fields
Richard Fitzpatrick
2014-06-27
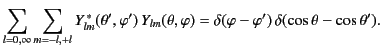

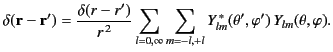

![$\displaystyle \left[\frac{d^{\,2}}{dr^{\,2}} +\frac{2}{r}\frac{d}{dr}+k^{\,2} -\frac{l\,(l+1)}{r^{\,2}}\right] g_l = - \frac{\delta(r-r')}{r^{\,2}}.$](img3180.png)